题目内容
如图，PA、PB是⊙O的切线，A、B分别为切点，PO交圆于点C，若∠APB=60°，PC=6，则AC的长为（ ）
A．4 B．
C．
D．
A．4 B．
C． D．D.
试题分析：如图，设CP交⊙O于点D，连接AD．设⊙O的半径为r．
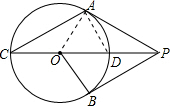
∵PA、PB是⊙O的切线，∠APB=60°，
∴OA⊥AP，∠APO=
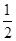∠APB=30°．∴OP=2OA，∠AOP=60°，
∴PC=2OA+OC=3r=6，则r=2，
易证△AOD是等边三角形，则AD=OA=2，
又∵CD是直径，
∴∠CAD=90°，
∴∠ACD=30°，
∴AC=AD•cot30°=2
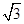
故选C．
考点: 切线的性质.
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
米，∠CAD＝30°，请你帮助文物学家完成下面两项工作：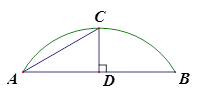
，AC=4，点O是AC的中点；回答下列问题：
，
，以点C为圆心，
为半径的圆交AB于点D，交AC于点E，则
的度数为( )
