题目内容
若直线y=k1x（k1≠0）和双曲线y=| k2 | x |
分析：明确一次函数中的k含义与反比例函数中k的含义是解题的关键，可用排除法．
解答：解：假设y=
中k2＞0，双曲线过第一，三象限，
则直线y=k1x应不过第一三象限，即k1需小于0，
反之k2＜0，则k1＞0，即k1、k2异号，
∴k1，k2的关系是k1•k2＜0．
| k2 |
| x |
则直线y=k1x应不过第一三象限，即k1需小于0，
反之k2＜0，则k1＞0，即k1、k2异号，
∴k1，k2的关系是k1•k2＜0．
点评：解决同一坐标系中两函数的系数关系问题，首先明确字母系数在不同函数解析式中的含义，分析字母的符号情况从而得出正确答案是必要条件．
练习册系列答案
相关题目
若直线y=k1x（k1≠0）和双曲线y=
（k2≠0）在同一直角坐标系中的图象无交点，则k1，k2的关系是（ ）
| k2 |
| x |
| A、互为倒数 | B、符号相同 |
| C、绝对值相等 | D、符号相反 |
若直线y=k1x（k1≠0）和双曲线y=
（k2≠0）在同一坐标系内的图象无交点，则k1、k2的关系是（ ）
| k2 |
| x |
| A、k1与k2异号 |
| B、k1与k2同号 |
| C、k1与k2互为倒数 |
| D、k1与k2的值相等 |
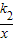（k2≠0）在同一直角坐标系中的图象无交点，则k1，k2的关系是（ ）