Question

【题目】如图，矩形的顶点和分别在轴和轴上，并且， ，反比例函数 (＞0)的图象交于点，交于点, 一次函数的图象经过点、，连结， .

（1）点的坐标是( )，点的坐标是( )；

（2）求反比例函数与一次函数的解析式；

（3）根据图象写出使得的的取值范围.

Answer 1

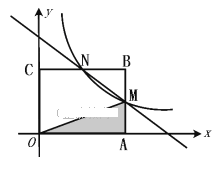
【答案】（1）点M的坐标是(4， )，点N的坐标是(2，3)

（2）反比例函数的解析式是，一次函数的解析式是；

（3）的取值范围是2＜＜4.

【解析】试题分析：（1）由， 可得出M点的横坐标和N点的纵坐标，由由此即可得出M纵坐标为，进而可求出N的坐标；

（2）将点M的坐标和N的坐标代入到中，解方程组即可求出a、b的值，进而求得一次函数的解析式；

（3）由图象即可求得x的取值范围.

试题解析：（1）∵，

∴点M的横坐标为4，

由，得×OA×AM=3，

∴AM=，

∴点M的坐标是(4， )，

∵，

∴N点的纵坐标为3，

由OA×AM=OC×NC，得NC=2，

∴点N的坐标是(2，3)；

（2）∵点N(2，3)在反比例函数 (x＞0)的图象上，

∴k=2×3=6即反比例函数的解析式是，

又∵y2=ax+b经过点M(4， )、N(2，3)

由此得： 解得

∴一次函数的解析式是

（3）若＜，则的取值范围是2＜＜4.