Question

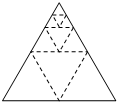将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，…如此继续下去，结果如下表：

所剪次数	1	2	3	4	…	n
正三角形个数	4	7	10	13	…	an

则剪10次时正三角形的个数a₁₀=________．

Answer 1

31
分析：从表格中的数据，不难发现：多剪一次，多3个三角形．继而即可求出剪10次时正三角形的个数．
解答：由图可知没剪的时候，有一个三角形，以后每剪一次就多出三个，所以总的正三角形的个数为3n+1．
当剪10次时正三角形的个数a₁₀=3×10+1=31．
故答案为：31．
点评：此类题属于找规律，难度适中，从所给数据中，很容易发现规律，再分析整理，得出结论．