题目内容
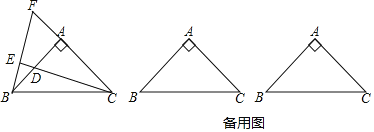
【题目】如图,在△ABC中,CD⊥AB于点D,AE⊥BC于点E,AE、CD交于点F,且∠DBF=45°.
(1)若AF=![]() ,BF=
,BF=![]() ,求AB的长;
,求AB的长;
(2)求证:AB﹣CF=![]() BF.
BF.

【答案】(1)AB=3;(2)见解析.
【解析】
(1)由等腰直角三角形的性质和勾股定理可求DF=BD=1,由勾股定理可求AD=2,即可求AB的长;
(2)由“AAS”可证△ADF≌△BCD,可得AD=CD,即可证等式成立.
(1)∵∠DBF=45°,CD⊥AB,
∴∠DFB=∠DBF=45°,
∵DF2+DB2=BF2,且BF=![]()
∴DF=BD=1,
在Rt△ADF中,AD=![]() =2,
=2,
∴AB=AD+DB=2+1=3;
(2))∵∠DBF=45°,CD⊥AB,
∴∠DFB=∠DBF=45°,
∴DF=DB,
∴BF=![]() DF,
DF,
∵AE⊥BC,CD⊥AB,
∴∠ABC+∠EAB=90°,∠ABC+∠DCB=90°,
∴∠EAB=∠DCB,且DF=DB,∠ADF=∠CDB=90°,
∴△ADF≌△BCD(AAS),
∴AD=CD,
∵AB﹣CF=AD+DB﹣CF=DF+BD=2DF=![]() BF
BF

练习册系列答案
相关题目