题目内容
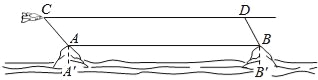
【题目】如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是60°,求两海岛间的距离AB.
【答案】(19000+300![]() )米.
)米.
【解析】
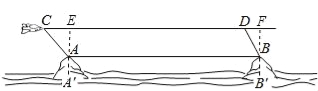
试题分析:首先过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,易得四边形ABFE为矩形,根据矩形的性质,可得AB=EF,AE=BF.由题意可知:AE=BF=1100﹣200=900米,CD=1.99×104米,然后分别在Rt△AEC与Rt△BFD中,利用三角函数即可求得CE与DF的长,从而求得CF,EF的长,继而求得两海岛间的距离AB.
试题解析:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,∵AB∥CD,∴∠AEF=∠EFB=∠ABF=90°,∴四边形ABFE为矩形.∴AB=EF,AE=BF.由题意可知:AE=BF=1100﹣200=900米,CD=1.99×104米=19900米.在Rt△AEC中,∠C=45°,AE=900米.∴CE=![]() =
=![]() =900(米). 在Rt△BFD中,∠BDF=60°,BF=900米.∴DF=
=900(米). 在Rt△BFD中,∠BDF=60°,BF=900米.∴DF=![]() =
=![]() =300
=300![]() (米).∴AB=EF=CD+DF﹣CE=19900+300
(米).∴AB=EF=CD+DF﹣CE=19900+300![]() ﹣900=19000+300
﹣900=19000+300![]() (米).所以两海岛间的距离AB为(19000+300
(米).所以两海岛间的距离AB为(19000+300![]() )米.
)米.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目