��Ŀ����
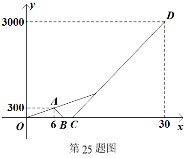
����Ŀ����ͼ��ֱ������ABCD�У�AD��BC��AB= ![]() cm��AD=24cm��BC=26cm����B=90�㣬����P��A��ʼ��AD����D��1cm/s���ٶ��˶�������Q�ӵ�C��ʼ��CB��3cm/s���ٶ����B�˶���P��Qͬʱ������������һ�㵽�ﶥ��ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊts���ʣ�
cm��AD=24cm��BC=26cm����B=90�㣬����P��A��ʼ��AD����D��1cm/s���ٶ��˶�������Q�ӵ�C��ʼ��CB��3cm/s���ٶ����B�˶���P��Qͬʱ������������һ�㵽�ﶥ��ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊts���ʣ� 
��1��t=ʱ���ı���PQCD��ƽ���ı��Σ�
��2���Ƿ����һ��tֵ��ʹPQ������ABCD�ֳ������ȵ������֣������������t��ֵ��
��3����tΪ��ֵʱ���ı���PQCDΪ�������Σ�
��4������DQ���Ƿ����tֵʹ��CDQΪ���������Σ���������ֱ��д��t��ֵ��
���𰸡�
��1��6
��2���⣺��AP+BQ=25ʱ��PQ������ABCD�ֳ������ȵ������֣�
��t+��26��3t��=25��
��ã�t= ![]()
��3���⣺��ͼ��

����D��DE��BC����CE=BC��AD=2cm��
��CQ��PD=4ʱ���ı���PQCD�ǵ������Σ�
��3t����24��t��=4��
��t=7��
��4���⣺���ڣ�t1=2��t2= ![]() ��t3=3��
��t3=3��
���������⣺��1��Ҫʹ�ı���PQCD��ƽ���ı��Σ���PD=CQ��
��3t=24��t����ã�t=6��
�����㾫����������Ҫ���������εĶ���͵������ε����ʵ����֪ʶ�㣬��Ҫ����һ��Ա�ƽ�У���һ��Ա߲�ƽ�е��ı��������Σ�������ȵ������ǵ������Σ��������ε�������ȣ�ͬһ���ϵ���������ȣ������Խ�����Ȳ�����ȷ�����⣮