题目内容
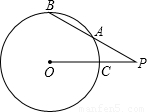
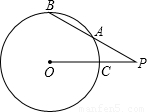
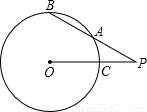
 如图,PAB为⊙O的割线,P0交⊙O于点C,OP=13,PA=9,AB=7,求⊙O直径的长.
如图,PAB为⊙O的割线,P0交⊙O于点C,OP=13,PA=9,AB=7,求⊙O直径的长.分析:延长PO到E,延长线与圆O交于点E,连接EB,AC.根据四边形ACEB为圆O的内接四边形,利用圆内接四边形的外角等于它的内对角得到一对角相等,再由公共角相等,利用两对对应角相等的两三角形相似,可得出△ACP与△EBP相似,由相似三角形的对应边成比例可以求得该圆的直径.
解答: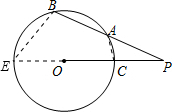 解:延长PO到E,延长线与圆O交于点E,连接EB,AC.
解:延长PO到E,延长线与圆O交于点E,连接EB,AC.
∵PA=9,AB=7,
∴PB=16.
∵四边形ACEB为圆O的内接四边形,
∴∠ACP=∠E,又∠P=∠P,
∴△ACP∽△EBP,
∴
=
,即
=
,
∴
=
,
解得:OC=5或x=-5 (舍去),
则EC=2OC=10,即⊙O直径的长是10.
 解:延长PO到E,延长线与圆O交于点E,连接EB,AC.
解:延长PO到E,延长线与圆O交于点E,连接EB,AC.∵PA=9,AB=7,
∴PB=16.
∵四边形ACEB为圆O的内接四边形,
∴∠ACP=∠E,又∠P=∠P,
∴△ACP∽△EBP,
∴
| PC |
| PB |
| PA |
| PE |
| PO-OC |
| 16 |
| 9 |
| PO+OC |
∴
| 13-OC |
| 16 |
| 9 |
| 13+OC |
解得:OC=5或x=-5 (舍去),
则EC=2OC=10,即⊙O直径的长是10.
点评:此题考查了圆内接四边形的性质,相似三角形的判定与性质,利用了转化及方程的思想,其中作出如图所示的辅助线是解本题的关键.

练习册系列答案
相关题目
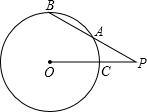 如图,PAB为⊙O的割线,且PA=AB=3,PO交⊙O于点C,若PC=2,则⊙O的半径的长为( )
如图,PAB为⊙O的割线,且PA=AB=3,PO交⊙O于点C,若PC=2,则⊙O的半径的长为( )A、
| ||
B、
| ||
C、
| ||
| D、7 |