题目内容
【题目】如图，在10×10正方形网格中，每个小正方形的边长均为1个单位长度．点B、C坐标分别为（﹣4，2）、（﹣1，2）．
（1）在图中建立平面直角坐标系，写出点A的坐标；
（2）将△ABC先向下平移4个单位，再向右平移5个单位得到△A1B1C1 ， 画出△A1B1C1 ， 并写出点C1的坐标；
（3）M（a，b）是△ABC内的一点，△ABC经过某种变换后点M的对应点为M2（a+1，b﹣7），画出△A2B2C2 ． 并求出△A2B2C2的面积．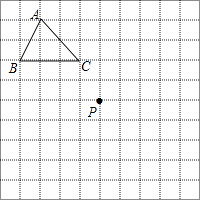
【答案】
（1）
解：建立平面直角坐标系，
如图1所示：
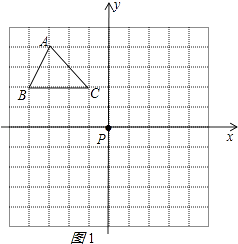
点A的坐标为（ 3，4 ）
（2）
解：如图2所示：
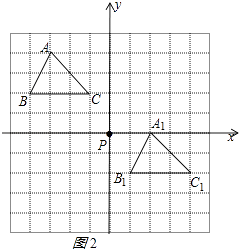
点C1的坐标为（ 4，﹣2 ）
（3）
解：如图3所示：
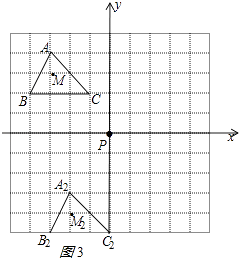
△A2B2C2的面积= 
×3×2=3
【解析】（1）由点B、C坐标容易建立平面直角坐标系，即可得出点A的坐标；（2）由平移的性质容易画出图形，得出点C1的坐标；（3）把△ABC先向下平移7个单位，再向右平移1个单位，即可得出△A2B2C2 ， 由三角形的面积公式容易求出△A2B2C2的面积．
练习册系列答案
相关题目
