题目内容
下列判断中:①负数没有立方根;②一个数的立方根有两个,它们互为相反数;③若x3=(-2)3,则x=2;④
18的立方根是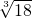 ;⑤任何有理数都有立方根,它不是正数就是负数.其中正确的个数有
;⑤任何有理数都有立方根,它不是正数就是负数.其中正确的个数有
- A.1个
- B.2个
- C.3个
- D.4个
B
分析:根据负数的立方根为负数,正数的立方根为正数,0的立方根为0对①②⑤进行判断;根据立方根的定义对③④进行判断.
解答:负数的立方根为负数,所以①正确;一个数的立方根有1个,所以②错误;若x3=(-2)3,则x=-2,所以③错误;18的立方根是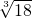 ,所以④正确;任何有理数都有立方根,0的立方根为0,所以⑤错误.
,所以④正确;任何有理数都有立方根,0的立方根为0,所以⑤错误.
故选B.
点评:本题考查了立方根:若一个数的立方等于a,那么这个数叫a的立方根,记作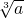 .
.
分析:根据负数的立方根为负数,正数的立方根为正数,0的立方根为0对①②⑤进行判断;根据立方根的定义对③④进行判断.
解答:负数的立方根为负数,所以①正确;一个数的立方根有1个,所以②错误;若x3=(-2)3,则x=-2,所以③错误;18的立方根是
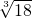 ,所以④正确;任何有理数都有立方根,0的立方根为0,所以⑤错误.
,所以④正确;任何有理数都有立方根,0的立方根为0,所以⑤错误.故选B.
点评:本题考查了立方根:若一个数的立方等于a,那么这个数叫a的立方根,记作
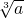 .
. 
练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目