题目内容
⊙O2与⊙O1交于A,B两点,射线O1A交⊙O2于C点,射线O2A交⊙O1于D点.求证:点A是△BCD的内心.
 证明:设两圆为⊙O、⊙Q,如图
证明:设两圆为⊙O、⊙Q,如图延长CA交⊙O1于M点,延长DA交⊙O2于N点,连接AB、DM、CN、MN,
∵AM是⊙O1的直径,AN是⊙O2的直径,
∴∠MDN=∠ACN=90°,
∴C、D、M、N四点共圆,
∴∠DMC=∠DNC,
∵∠DMC=∠DBA,∠DNC=∠ABC,
∴∠DBA=∠ABC,
∴点A在∠DBC的角平分线上,
∵C、D、M、N四点共圆,
∴∠DCM=∠DNM,
∵∠DNM=∠ACB,
∴∠DCM=∠ACB,
∴点A在∠DCB的角平分线上,
同理:点A在∠CDB的角平分线上,
∴点A是△CDB的三个角平分线的交点,
∴点A是△BCD的内心.
分析:首先作辅助线延长CA交⊙O1于M点,延长DA交⊙O2于N点,连接AB、DM、CN、MN,证出C、D、M、N四点共圆,再推出点A在∠DBC的角平分线上,同理点A也在∠DCB和∠CDB的角平分线上,即可得出答案.
点评:本题主要考查了四点共圆,圆周角定理,三角形的内切圆和内心,确定圆的条件等知识点,作辅助线证C、D、M、N四点共圆是解此题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
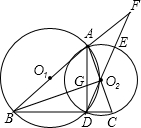 ⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA延长线于F,BO2交AD于G,连接AD.
⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA延长线于F,BO2交AD于G,连接AD.