题目内容
已知两等圆⊙O1与⊙O2相交于A、B两点,过点B作任意直线分别与⊙O1交于点C,与⊙O2交于点D.(1)试判别△ACD的形状,并证明你的结论成立;
(2)两圆再满足什么条件时,△ACD为等边三角形?(要求:画出图形,并证明)
分析:(1)根据等圆的定义和圆心角、弧、弦之间的关系得到∠C=∠D,根据等腰三角形性质推出即可;
(2)根据等圆定义得到等边三角形,推出∠AO1O2=60°,得到∠C=60°,根据等边三角形的判定即可推出答案.
(2)根据等圆定义得到等边三角形,推出∠AO1O2=60°,得到∠C=60°,根据等边三角形的判定即可推出答案.
解答:证明:△ACD为等腰三角形.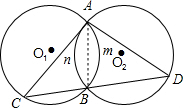
(1)∵⊙O1,⊙O2为等圆,AB=AB,
∴
=
∴∠C=∠D,
∴AC=AD,
∴△ACD是等腰三角形.
(2)解:当⊙O1过O2点时(或⊙O2过O1点),△ACD为等边三角形.
证明:∵连接O1A、O1O2、O2A、O2B,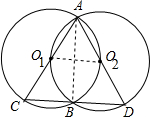
∵⊙O1、⊙O2是等圆,
∴O1A=O1O2=O2A,
∴△AO1O2是等边三角形,
∴∠AO1O2=60°,
又∵AB=2AO2,
∵∠C=∠AO1O2=60°,
又∵AC=AD,
∴△ACD为等边三角形.

(1)∵⊙O1,⊙O2为等圆,AB=AB,
∴
 |
| AmB |
 |
| AnB |
∴∠C=∠D,
∴AC=AD,
∴△ACD是等腰三角形.
(2)解:当⊙O1过O2点时(或⊙O2过O1点),△ACD为等边三角形.
证明:∵连接O1A、O1O2、O2A、O2B,

∵⊙O1、⊙O2是等圆,
∴O1A=O1O2=O2A,
∴△AO1O2是等边三角形,
∴∠AO1O2=60°,
又∵AB=2AO2,
∵∠C=∠AO1O2=60°,
又∵AC=AD,
∴△ACD为等边三角形.
点评:本题主要考查对相交两圆的性质,圆心角、弧、弦之间的关系,等边三角形的判定,等腰三角形的性质等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
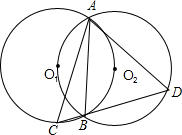 ?若成立,给出证明;若不成立,那么AC和AD的长与两圆半径有什么关系?说明理由.
?若成立,给出证明;若不成立,那么AC和AD的长与两圆半径有什么关系?说明理由. 30、如图,已知两个等圆⊙O1与⊙O2相交于A、B两点,一条直线经过点A,分别与两圆相交于点C、D,MC切⊙O1于点C,MD切⊙O2于点D,若∠BCD=30°,则∠M等于
30、如图,已知两个等圆⊙O1与⊙O2相交于A、B两点,一条直线经过点A,分别与两圆相交于点C、D,MC切⊙O1于点C,MD切⊙O2于点D,若∠BCD=30°,则∠M等于