题目内容
已知矩形纸片ABCD中,AB=1,BC=2,将该纸片叠成一个平面图形,折痕EF不经过A点(E、F是该矩形边界上的点),折叠后点A落在A′处,给出以下判断:
①当四边形A,CDF为正方形时,EF=
②当EF= 时,四边形A′CDF为正方形
时,四边形A′CDF为正方形
③当EF=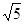 时,四边形BA′CD为等腰梯形;
时,四边形BA′CD为等腰梯形;
④当四边形BA′CD为等腰梯形时,EF=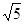 。
。
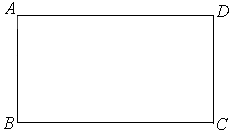
其中正确的是 (把所有正确结论序号都填在横线上)。
①当四边形A,CDF为正方形时,EF=

②当EF=
 时,四边形A′CDF为正方形
时,四边形A′CDF为正方形③当EF=
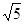 时,四边形BA′CD为等腰梯形;
时,四边形BA′CD为等腰梯形;④当四边形BA′CD为等腰梯形时,EF=
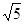 。
。
其中正确的是 (把所有正确结论序号都填在横线上)。
①③④。
根据相关知识逐一作出判断:
①∵AB=1,BC=2,∴如图,
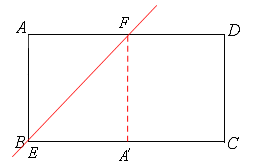
当四边形A′CDF为正方形时,A′C="CD=" A′F=2,A′F⊥BC。
∴A′E=2。∴根据勾股定理得EF=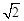 。判断①正确。
。判断①正确。
②当EF=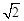 时,由①知,只要EF与AB成450角即可,此时的EF与①中的EF平行即可,这时,除①的情况外,其它都不构成正方形。判断①错误。
时,由①知,只要EF与AB成450角即可,此时的EF与①中的EF平行即可,这时,除①的情况外,其它都不构成正方形。判断①错误。
③当EF=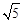 时,由勾股定理知BD=
时,由勾股定理知BD=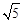 ,∴此时,EF与BD重合。
,∴此时,EF与BD重合。
由折叠对称和矩形的性质知,CD="AB=" A′B,且CD与 A′B不平行。
如图,
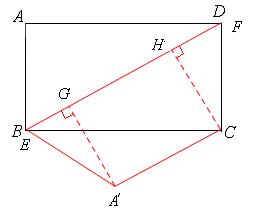
过点A′作A′G⊥BD于点G,过点C作CH⊥BD于点FH,则
∵A′B=CD,∠A′BG=∠ABD=∠CDH,∠A′GB =∠CND,
∴△A′GB≌△CHD(AAS)。∴A′G=CH。∴A′C∥BD。
∴四边形BA′CD为等腰梯形。判断③正确。
④当四边形BA′CD为等腰梯形时,由A′B=CD,∠A′BD=∠CDB=∠ABD,知点A′是点A关于BD的对称点,即A′是点A沿BD折叠得到,所以,EF与BD重合,EF=BD=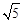 。判断④正确。
。判断④正确。
综上所述,判断正确的是①③④。
①∵AB=1,BC=2,∴如图,

当四边形A′CDF为正方形时,A′C="CD=" A′F=2,A′F⊥BC。
∴A′E=2。∴根据勾股定理得EF=
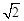 。判断①正确。
。判断①正确。②当EF=
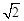 时,由①知,只要EF与AB成450角即可,此时的EF与①中的EF平行即可,这时,除①的情况外,其它都不构成正方形。判断①错误。
时,由①知,只要EF与AB成450角即可,此时的EF与①中的EF平行即可,这时,除①的情况外,其它都不构成正方形。判断①错误。③当EF=
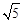 时,由勾股定理知BD=
时,由勾股定理知BD=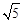 ,∴此时,EF与BD重合。
,∴此时,EF与BD重合。由折叠对称和矩形的性质知,CD="AB=" A′B,且CD与 A′B不平行。
如图,

过点A′作A′G⊥BD于点G,过点C作CH⊥BD于点FH,则
∵A′B=CD,∠A′BG=∠ABD=∠CDH,∠A′GB =∠CND,
∴△A′GB≌△CHD(AAS)。∴A′G=CH。∴A′C∥BD。
∴四边形BA′CD为等腰梯形。判断③正确。
④当四边形BA′CD为等腰梯形时,由A′B=CD,∠A′BD=∠CDB=∠ABD,知点A′是点A关于BD的对称点,即A′是点A沿BD折叠得到,所以,EF与BD重合,EF=BD=
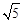 。判断④正确。
。判断④正确。综上所述,判断正确的是①③④。

练习册系列答案
相关题目

 的值是 .
的值是 .
 ,设AB=x,AD=y。
,设AB=x,AD=y。

 在线段
在线段 上,
上, ,
, ,
, .
.
 ;
;  的形状,并证明你的结论.
的形状,并证明你的结论.