题目内容
【题目】完成下面的证明。
已知:如图,BE∥CD,∠A=∠1,
求证:∠C=∠E。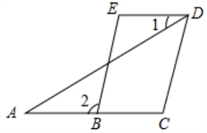
证明:∵BE∥CD (已知 )
∴∠2=∠C ( )
又 ∵∠A=∠1 (已知 )
∴ AC∥DE ( )
∴ ∠2=∠E( )
∴∠C=∠E ( )
【答案】证明:∵BE∥CD (已知 )
∴∠2=∠C ( 两直线平行,同位角相等 )
又 ∵∠A=∠1 (已知 )
∴ AC∥DE ( 内错角相等,两直线平行 )
∴ ∠2=∠E( 两直线平行,内错角相等 )
∴∠C=∠E ( 等量代换 )
【解析】由BE//CD 得∠2=∠C,根据是两直线平行,同位角相等;而∠1=∠A得AC∥DE,根据是内错角相等,两直线平行;再根据两直线平行,内错角相等得∠2=∠E,由等量代换 即可得到结论.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目