题目内容
(2012•随州)一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动,快车离乙地的路程y1(km)与行使的时间x(h)之间的函数关系,如图中AB所示;慢车离乙地的路程y2(km)与行使的时间x(h)之间的函数关系,如图中线段OC所示,根据图象进行以下研究.
解读信息:
(1)甲,乙两地之间的距离为
(2)线段AB的解析式为
问题解决:
(3)设快,慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数图象.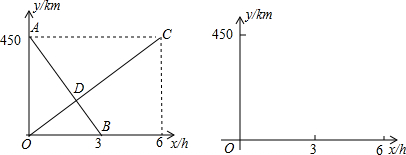
解读信息:
(1)甲,乙两地之间的距离为
450
450
km;(2)线段AB的解析式为
y1=450-150x(0≤x≤3)
y1=450-150x(0≤x≤3)
;线段OC的解析式为y2=75x (0≤x≤6)
y2=75x (0≤x≤6)
;问题解决:
(3)设快,慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数关系式,并画出函数图象.

分析:(1)利用A点坐标为(0,450),可以得出甲,乙两地之间的距离;
(2)利用A点坐标为(0,450),B点坐标为(3,0),代入y1=kx+b求出即可,利用线段OC解析式为y2=ax 求出a即可;
(3)利用(2)中所求得出,y=|y1-y2|进而求出函数解析式,得出图象即可.
(2)利用A点坐标为(0,450),B点坐标为(3,0),代入y1=kx+b求出即可,利用线段OC解析式为y2=ax 求出a即可;
(3)利用(2)中所求得出,y=|y1-y2|进而求出函数解析式,得出图象即可.
解答: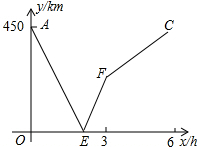 解:(1)根据左图可以得出:甲、乙两地之间的距离为450km;
解:(1)根据左图可以得出:甲、乙两地之间的距离为450km;
故答案为:450km;
(2)问题解决:线段AB的解析式为:y1=kx+b,根据A点坐标为(0,450),B点坐标为(3,0),
得出:
,
解得:
故y1=450-150x(0≤x≤3);
将(6,450)代入y2=ax 求出即可:
y2=75x,
故线段OC的解析式为 y2=75x (0≤x≤6);
(3)根据(2)得出:
y=|y1-y2|=|450-150x-75x|=
,
利用函数解析式y=450-225x(0≤x≤2),当x=0,y=450,x=2,y=0,画出线段AE,
利用函数解析式y=225x-450(2≤x<3),当x=2,y=0,x=3,y=225,画出线段EF,
利用函数解析式y=75x(3≤x≤6),当x=3,y=225,x=6,y=450,画出线段FC,
求出端点,画出图象,其图象为折线图AE-EF-FC.
 解:(1)根据左图可以得出:甲、乙两地之间的距离为450km;
解:(1)根据左图可以得出:甲、乙两地之间的距离为450km;故答案为:450km;
(2)问题解决:线段AB的解析式为:y1=kx+b,根据A点坐标为(0,450),B点坐标为(3,0),
得出:
|
解得:
|
故y1=450-150x(0≤x≤3);
将(6,450)代入y2=ax 求出即可:
y2=75x,
故线段OC的解析式为 y2=75x (0≤x≤6);
(3)根据(2)得出:
y=|y1-y2|=|450-150x-75x|=
|
利用函数解析式y=450-225x(0≤x≤2),当x=0,y=450,x=2,y=0,画出线段AE,
利用函数解析式y=225x-450(2≤x<3),当x=2,y=0,x=3,y=225,画出线段EF,
利用函数解析式y=75x(3≤x≤6),当x=3,y=225,x=6,y=450,画出线段FC,
求出端点,画出图象,其图象为折线图AE-EF-FC.
点评:此题主要考查了一次函数的应用和待定系数法求解析式,根据已知图象上的点得出函数解析式以及利用分段函数分析是解题关键.

练习册系列答案
相关题目
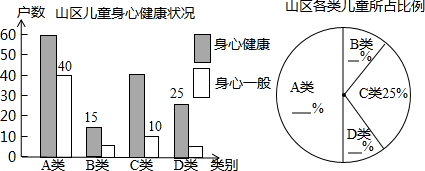
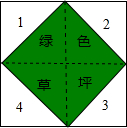 (2012•随州)如图所示,一个大正方形地面上,编号为1,2,3,4的地块,是四个全等的等腰直角三角形空地,中间是小正方形绿色草坪,一名训练有素的跳伞运动员,每次跳伞都能落在大正方形地面上.
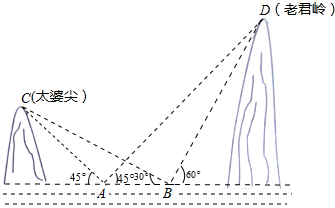
(2012•随州)如图所示,一个大正方形地面上,编号为1,2,3,4的地块,是四个全等的等腰直角三角形空地,中间是小正方形绿色草坪,一名训练有素的跳伞运动员,每次跳伞都能落在大正方形地面上. (2012•随州)在一次数学活动课上,老师出了一道题:
(2012•随州)在一次数学活动课上,老师出了一道题: