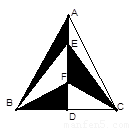题目内容
如图,在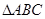 中,AB=AC,以AB为直径的
中,AB=AC,以AB为直径的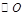 交BC于点M,
交BC于点M,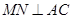 于点N.
于点N.
(1)求证:MN是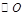 的切线;(2)若
的切线;(2)若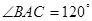 ,AB=2,求图中阴影部分的面积.
,AB=2,求图中阴影部分的面积.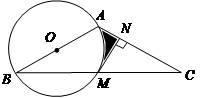
(1)证明MN是 的切线,即证明MN⊥OM,可通过证明OM∥AC,因为MN⊥AC,那么MN⊥OM,M在圆上,且OM为⊙O的半径,则说明MN是
的切线,即证明MN⊥OM,可通过证明OM∥AC,因为MN⊥AC,那么MN⊥OM,M在圆上,且OM为⊙O的半径,则说明MN是 的切线.
的切线.
(2)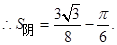
解析试题分析:(1)证明:连接OM.
∵AB=AC
∴∠B=∠C
∵OM=OB
∴∠B=∠OMB
∴∠C=∠OMB
∴OM∥AC
∵MN⊥AC
∴MN⊥OM
又∵M在⊙上
且OM为⊙O的半径
∴MN是⊙O的切线.
(2)连AM.
∵AB是⊙O的直径
∴∠AMB=90°
即AM⊥BC
又∵∠BAC=120°
∴∠BAM=∠CAM=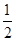 ∠BAC=60°
∠BAC=60°
∴△AOM为等边三角形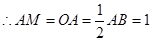 .
.
在R t △AMN中,∠AMN=30°,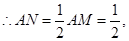
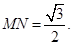
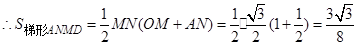
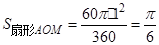
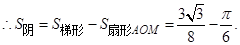
考点:圆切线的证明和求不规则图形面积
点评:该题是常考题,主要考查学生对圆相关性质的理解和应用以及掌握圆切线的证明方法,不规则图形的面积通常用割补法计算。

练习册系列答案
相关题目

 中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是
中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是 
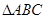 中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是
中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是 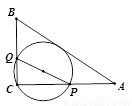
 中,AB=AC,D是底边BC的中点, 作DE⊥AB于E,DF⊥AC于F求证:DE=DF.
中,AB=AC,D是底边BC的中点, 作DE⊥AB于E,DF⊥AC于F求证:DE=DF.
 中,AB=AC=5,BC=6,点E,F是中线AD上的两点,则图中阴影部分的面积是( )
中,AB=AC=5,BC=6,点E,F是中线AD上的两点,则图中阴影部分的面积是( )