题目内容
【题目】如图，将△ABC绕点B逆时针旋转40°，得到△A′B′C′，若点C′恰好落在边BA的延长线上，且A′C′∥BC，连接CC′，则∠ACC′=度．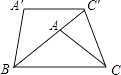
【答案】30
【解析】解：∵△ABC绕点B逆时针旋转40°，
∴∠CAC′=40°，BC=BC′，∠ACB=∠A′C′B，
∵A′C′∥BC，
∴∠A′C′B=∠CAC′=40°，
∴∠ACB=40°，
∵BC=BC′，
∴∠BCC′=∠BC′C，
∴∠BCC′= 
（180°﹣40°）=70°，
∴∠ACC′=∠BCC′﹣∠ACB=70°﹣40°=30°．
所以答案是30．
【考点精析】本题主要考查了平行线的性质和三角形的内角和外角的相关知识点，需要掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题．
练习册系列答案
每课必练系列答案
相关题目
【题目】在“元旦”期间，平价商场对该商场商品进行如下的优惠促销活动：
打折前一次性购物总金额 | 优惠措施 |
小于等于 400 元 | 不优惠 |
超过 400 元，但不超过 600元 | 按售价打九折 |
超过 600 元 | 其中 600 元部分八折优惠，超过 600 元的部分打六折优惠 |
按上述优惠条件，若小华一次性购买售价为 80 元/件的商品 n 件时，实际付款 504 元， 则 n=_____.
