题目内容
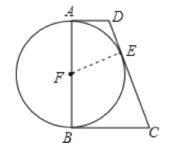
【题目】如图:在直角梯形四ABCD中,AD∥BC,∠B=90°,以AB为直径的圆F切DC于点E. 若圆F的半径是6cm,AD=4cm,求梯形ABCD的面积.
【答案】78cm2.
【解析】
连接DF、CF,由切线长定理可得DE=AD=4,BC=CE,结合条件可证得∠DFC=90°,可证明△DEF∽△FEC,可求得CE,再由梯形的面积可求出答案.
如图,连接DF、CF,
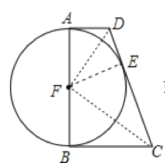
∵∠DAB=∠FBC=90°,
∴DA、BC为圆F的切线,且CD为圆F的切线,
∴FE⊥CD,且DE=AD=4cm,CE=BC,
由切线长定理可得∠ADF=∠EDF,
∴∠AFD=∠DFE,同理可得∠EFC=∠BFC,
∴∠DFC=90°,
∴△DEF∽△FEC,
∴![]() ,即
,即![]() ,
,
∴EC=9cm,
∴BC=EC=9cm,
∴S![]() =
=![]() (AD+BC)AB=
(AD+BC)AB=![]() ×(4+9)×12=78(cm
×(4+9)×12=78(cm![]() ).
).

练习册系列答案
相关题目