题目内容
如图所示,将矩形OABC沿AE折叠,使点O恰好落在BC上F处,以CF为边作正方形CFGH,延长BC至M,使CM=|CE-EO|,再以CM、CO为边作矩形CMNO.令m=
,则m=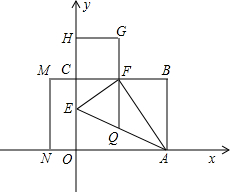 CO=1,CE=
CO=1,CE=
,Q为AE上一点且QF=
,抛物线y=mx2+bx+c经过C、Q两点,则抛物线与边AB的交点坐标是
| S四边形CFGH |
| S四边形CMNO |
1
1
;又若 CO=1,CE=
CO=1,CE=| 1 |
| 3 |
| 2 |
| 3 |
(
,
)
2
| ||
| 3 |
| 1 |
| 3 |
(
,
)
.2
| ||
| 3 |
| 1 |
| 3 |
分析:求出CM=OE-CE,求出四边形CFGH的面积是CO×(OE-CE),求出四边形CMNO的面积是(OE-CE)×CO,即可求出m值;求出EF值,得出EF=QF,得出等边三角形EFQ,求出EQ,求出∠CEF、∠OEA,过Q作QD⊥OE于D,求出Q坐标,代入抛物线求出抛物线的解析式,把x=
代入抛物线即可求出y,即得出答案.
2
| ||
| 3 |
解答:解:∵沿AE折叠,O和F重合,
∴OE=EF,
∵在Rt△CEF中,EF>CE,
即OE>CE,
∴CM=|CE-EO|=OE-CE,
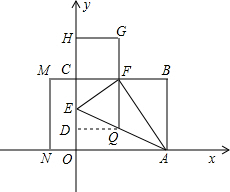 ∵S四边形CFGH=CF2=EF2-EC2=EO2-EC2=(EO+EC)(EO-EC)=CO×(EO-EC),
∵S四边形CFGH=CF2=EF2-EC2=EO2-EC2=(EO+EC)(EO-EC)=CO×(EO-EC),
S四边形CMNO=CM×CO=(OE-CE)×OC,
∴m=
=1;
∵CO=1,CE=
,QF=
,
∴EF=EO=
=QF,C(0,1),
∴sin∠EFC=
=
,
∴∠EFC=30°,∠CEF=60°,
∴∠FEA=
×(180°-60°)=60°,
∵EF=QF,
∴△EFQ是等边三角形,
∴EQ=
,
过Q作QD⊥OE于D,
ED=
EQ=
.
∵由勾股定理得:DQ=
,
∴OD=
-
=
,
即Q的坐标是(
,
),
∵抛物线过C、Q,m=1代入得:
,
解得:b=-
,c=1,
∴抛物线的解析式是:y=x2-
x+1,
AO=
EO=
,
∵把x=
代入抛物线得:y=
,
∴抛物线与AB的交点坐标是(
,
),
故答案为:1,(
,
).
∴OE=EF,
∵在Rt△CEF中,EF>CE,
即OE>CE,
∴CM=|CE-EO|=OE-CE,
 ∵S四边形CFGH=CF2=EF2-EC2=EO2-EC2=(EO+EC)(EO-EC)=CO×(EO-EC),
∵S四边形CFGH=CF2=EF2-EC2=EO2-EC2=(EO+EC)(EO-EC)=CO×(EO-EC),S四边形CMNO=CM×CO=(OE-CE)×OC,
∴m=
| S四边形CFGH |
| S四边形CMNO |
∵CO=1,CE=
| 1 |
| 3 |
| 2 |
| 3 |
∴EF=EO=
| 2 |
| 3 |
∴sin∠EFC=
| CE |
| EF |
| 1 |
| 2 |
∴∠EFC=30°,∠CEF=60°,
∴∠FEA=
| 1 |
| 2 |
∵EF=QF,
∴△EFQ是等边三角形,
∴EQ=
| 2 |
| 3 |
过Q作QD⊥OE于D,
ED=
| 1 |
| 2 |
| 1 |
| 3 |
∵由勾股定理得:DQ=
| ||
| 3 |
∴OD=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
即Q的坐标是(
| ||
| 3 |
| 1 |
| 3 |
∵抛物线过C、Q,m=1代入得:
|
解得:b=-
| 3 |
∴抛物线的解析式是:y=x2-
| 3 |
AO=
| 3 |
2
| ||
| 3 |
∵把x=
2
| ||
| 3 |
| 1 |
| 3 |
∴抛物线与AB的交点坐标是(
2
| ||
| 3 |
| 1 |
| 3 |
故答案为:1,(
2
| ||
| 3 |
| 1 |
| 3 |
点评:本题考查了勾股定理,用待定系数法求二次函数的解析式,等边三角形的性质和判定,轴对称的性质,含30度角的直角三角形性质的应用,主要考查学生综合运用性质进行推理和计算的能力,题目比较好,但是有一定的难度.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
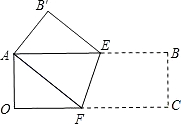
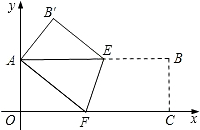


 已知,如图所示,矩形OABC在平面直角坐标系中,矩形各顶点分别为O(0,0),A(0,6),B(8,6),C(8,0).点D(0,3)在OA上,点E(4,0)在OC上,连接DE,将△DOE绕O点逆时针旋转,旋转角为α(0°<α<360°),得到△D′OE′,连接AD′,当∠AD′O=90°时,
已知,如图所示,矩形OABC在平面直角坐标系中,矩形各顶点分别为O(0,0),A(0,6),B(8,6),C(8,0).点D(0,3)在OA上,点E(4,0)在OC上,连接DE,将△DOE绕O点逆时针旋转,旋转角为α(0°<α<360°),得到△D′OE′,连接AD′,当∠AD′O=90°时, 在直角坐标系中,OA=6,OC=8,若将矩形折叠,使点B与O重合,得到折痕EF。
在直角坐标系中,OA=6,OC=8,若将矩形折叠,使点B与O重合,得到折痕EF。 
