题目内容
如图,在矩形OABC中,AB=2BC,点A在y轴的正半轴上,点C在x轴的正半轴上,连接OB,反比例函数 (k≠0,x>0)的图象经过OB的中点D,与BC边交于点E,点E的横坐标是4,则k的值是
(k≠0,x>0)的图象经过OB的中点D,与BC边交于点E,点E的横坐标是4,则k的值是
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:∵在矩形OABC中,AB=2BC,点D是OB的中点,点E在BC边上,点E的横坐标是4,
∴D点横坐标为:2,AB=OC=4,BC= AB=2。
AB=2。
∴D点纵坐标为:1。
∵反比例函数 (k≠0,x>0)的图象经过点D,
(k≠0,x>0)的图象经过点D,
∴k=xy=1×2=2。
故选B。

练习册系列答案
相关题目
已知点A(1,y1)、B(2,y2)、C(﹣3,y3)都在反比例函数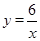 的图象上,则y1、y2、y3的大小关系是( )
的图象上,则y1、y2、y3的大小关系是( )
| A.y3<y1<y2 | B.y1<y2<y3 | C.y2<y1<y3 | D.y3<y2<y1 |
图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )
| A.当x=3时,EC<EM | B.当y=9时,EC>EM |
| C.当x增大时,EC•CF的值增大 | D.当y增大时,BE•DF的值不变 |
若反比例函数 的图象上有两点P1(2,y1)和P2(3,y2),那么
的图象上有两点P1(2,y1)和P2(3,y2),那么
| A.y1<y2<0 | B.y1>y2>0 | C.y2<y1<0 | D.y2>y1>0 |
如图,直线y=2x与双曲线 在第一象限的交点为A,过点A作AB⊥x轴于B,将△ABO绕点O旋转90°,得到△A′B′O,则点A′的坐标为
在第一象限的交点为A,过点A作AB⊥x轴于B,将△ABO绕点O旋转90°,得到△A′B′O,则点A′的坐标为
| A.(1.0) | B.(1.0)或(﹣1.0) |
| C.(2.0)或(0,﹣2) | D.(﹣2.1)或(2,﹣1) |
某地资源总量Q一定,该地人均资源享有量 与人口数
与人口数 的函数关系图象是
的函数关系图象是
A. | B. | C. | D. |
下列四个点中,在反比例函数 的图象上的是【 】
的图象上的是【 】
| A.(3,﹣2) | B.(3,2) | C.(2,3) | D.(﹣2,﹣3) |
 的图象经过点A,反比例函数
的图象经过点A,反比例函数 的图象经过点B,则下列关于m,n的关系正确的是
的图象经过点B,则下列关于m,n的关系正确的是



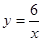 的图象上,则y1、y2、y3的大小关系是____________________.
的图象上,则y1、y2、y3的大小关系是____________________.