题目内容
(2012•恩施州)小丁每天从某报社以每份0.5元买进报纸200份,然后以每份1元卖给读者,报纸卖不完,当天可退回报社,但报社只按每份0.2元退给小丁,如果小丁平均每天卖出报纸x份,纯收入为y元.
(1)求y与x之间的函数关系式(要求写出自变量x的取值范围);
(2)如果每月以30天计算,小丁每天至少要卖多少份报纸才能保证每月收入不低于2000元?
(1)求y与x之间的函数关系式(要求写出自变量x的取值范围);
(2)如果每月以30天计算,小丁每天至少要卖多少份报纸才能保证每月收入不低于2000元?
分析:(1)因为小丁每天从某市报社以每份0.5元买出报纸200份,然后以每份1元卖给读者,报纸卖不完,当天可退回报社,但报社只按每份0.2元退给小丁,所以如果小丁平均每天卖出报纸x份,纯收入为y元,则y=(1-0.5)x-(0.5-0.2)(200-x)即y=0.8x-60,其中0≤x≤200且x为整数;
(2)因为每月以30天计,根据题意可得30(0.8x-60)≥2000,解之即可求解.
(2)因为每月以30天计,根据题意可得30(0.8x-60)≥2000,解之即可求解.
解答:解:(1)y=(1-0.5)x-(0.5-0.2)(200-x)
=0.8x-60(0≤x≤200);
(2)根据题意得:
30(0.8x-60)≥2000,
解得x≥158
.
故小丁每天至少要卖159份报纸才能保证每月收入不低于2000元.
=0.8x-60(0≤x≤200);
(2)根据题意得:
30(0.8x-60)≥2000,
解得x≥158
| 1 |
| 3 |
故小丁每天至少要卖159份报纸才能保证每月收入不低于2000元.
点评:此题主要考查了一次函数的应用,首先要正确理解题意,然后仔细分析题意,正确列出函数关系式,最后利用不等式即可解决问题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
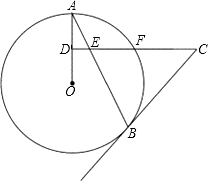 (2012•恩施州)如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(2012•恩施州)如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.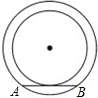 (2012•恩施州)如图,两个同心圆的半径分别为4cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
(2012•恩施州)如图,两个同心圆的半径分别为4cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )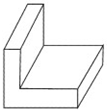 (2012•恩施州)一个用于防震的L形包装塑料泡沫如图所示,则该物体的俯视图是( )
(2012•恩施州)一个用于防震的L形包装塑料泡沫如图所示,则该物体的俯视图是( )