题目内容
如下左图,四边形ABCD与四边形EFGH相似,则∠G= .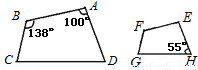
【答案】分析:观察图形,根据相似多边形的对应角相等得出∠D=∠H,再根据四边形的内角和等于360°计算求出∠C,再根据相似多边形的对应角相等即可求解.
解答:解:∵四边形ABCD与四边形EFGH相似,
∴∠D=∠H=55°,
在四边形ABCD中,∠C=360°-138°-100°-55°=67°.
∴∠G=∠C=67°.
故答案为:67°.
点评:本题考查了相似多边形的对应角相等的性质,四边形的内角和等于360°,熟记性质与公式是求解的关键.
解答:解:∵四边形ABCD与四边形EFGH相似,
∴∠D=∠H=55°,
在四边形ABCD中,∠C=360°-138°-100°-55°=67°.
∴∠G=∠C=67°.
故答案为:67°.
点评:本题考查了相似多边形的对应角相等的性质,四边形的内角和等于360°,熟记性质与公式是求解的关键.

练习册系列答案
相关题目