题目内容
【题目】如图，矩形OABC的顶点A、C分别在x、y的正半轴上，点B的坐标为（3，4），一次函数 
的图象与边OC、AB分别交于点D、E，并且满足OD=BE．点M是线段DE上的一个动点．
（1）求b的值；
（2）连结OM，若三角形ODM的面积与四边形OAEM的面积之比为1：3，求点M的坐标；
（3）设点N是x轴上方平面内的一点，以O、D、M、N为顶点的四边形是菱形，求点N的坐标．
【答案】
（1）
解： 
中，令x=0，解得y=b，则D的坐标是（0，b），OD=b，
∵OD=BE，
∴BE=b，则E的坐标是（3，4﹣b），
把E的坐标代入 得4﹣b=﹣2+b，
解得：b=3
（2）
解：S四边形OAED= 
（OD+AE）OA= ×（3+1）×3=6，
∵三角形ODM的面积与四边形OAEM的面积之比为1：3，
∴S△ODM=1.5．
设M的横坐标是a，则 ×3a=1.5，
解得：a=1，
把x=a=1代入y=﹣ 
x+3得y=﹣ × 
+3= 
．
则M的坐标是（1， ）
（3）
解：当四边形OMDN是菱形时，如图（1），
M的纵坐标是 
，把y= 代入y=﹣ x+3，得﹣ x+3= ，解得：x= 
，
则M的坐标是（ ， ），
则N的坐标是（﹣ ， ）；
当四边形OMND是菱形时，如图（2）
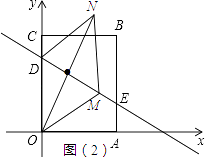
OM=OD=3，设M的横坐标是m，则纵坐标是﹣ m+3，
则m2+（﹣ m+3）2=9，
解得：m= 
或0（舍去）．
则M的坐标是（ 
， 
）．
则DM的中点是（ 
， 
）．
则N的坐标是（ ， 
）．
故N的坐标是（﹣ ， ）或（ ， ）．
【解析】（1）首先在一次函数的解析式中令x=0，即可求得D的坐标，则OD的长度即可求得，OD=b，则E的坐标即可利用b表示出来，然后代入一次函数解析式即可得到关于b的方程，求得b的值；（2）首先求得四边形OAED的面积，则△ODM的面积即可求得，设出M的横坐标，根据三角形的面积公式即可求得M的横坐标，进而求得M的坐标；（3）分成四边形OMDN是菱形和四边形OMND是菱形两种情况进行讨论，四边形OMDN是菱形时，M是OD的中垂线与DE的交点，M关于OD的对称点就是N；
四边形OMND是菱形，OM=OD，M在直角DE上，设出M的坐标，根据OM=OD即可求得M的坐标，则根据ON和DM的中点重合，即可求得N的坐标．
【考点精析】根据题目的已知条件，利用菱形的性质和矩形的性质的相关知识可以得到问题的答案，需要掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半；矩形的四个角都是直角，矩形的对角线相等．
