题目内容
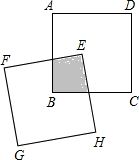 (2012•岳阳)如图,两个边长相等的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E顺时针方向旋转,设它们重叠部分的面积为S,旋转的角度为θ,S与θ的函数关系的大致图象是( )
(2012•岳阳)如图,两个边长相等的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E顺时针方向旋转,设它们重叠部分的面积为S,旋转的角度为θ,S与θ的函数关系的大致图象是( )分析:过点E作EM⊥BC于点M,EN⊥AB于点N,则可证明△ENK≌△EML,从而得出重叠部分的面积不变,继而可得出函数关系图象.
解答: 解:如右图,过点E作EM⊥BC于点M,EN⊥AB于点N,
解:如右图,过点E作EM⊥BC于点M,EN⊥AB于点N,
∵点E是正方形的对称中心,
∴EN=EM,
由旋转的性质可得∠NEK=∠MEL,
在Rt△ENK和Rt△EML中,
,
故可得△ENK≌△EML,即阴影部分的面积始终等于正方形面积的
.
故选B.
 解:如右图,过点E作EM⊥BC于点M,EN⊥AB于点N,
解:如右图,过点E作EM⊥BC于点M,EN⊥AB于点N,∵点E是正方形的对称中心,
∴EN=EM,
由旋转的性质可得∠NEK=∠MEL,
在Rt△ENK和Rt△EML中,
|
故可得△ENK≌△EML,即阴影部分的面积始终等于正方形面积的
| 1 |
| 4 |
故选B.
点评:此题考查了动点问题的函数图象,证明△ENK≌△EML,得出阴影部分的面积始终等于正方形面积的
是解答本题的关键.
| 1 |
| 4 |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
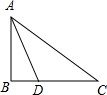 (2012•岳阳)如图,在Rt△ABC中,∠B=90°,沿AD折叠,使点B落在斜边AC上,若AB=3,BC=4,则BD=
(2012•岳阳)如图,在Rt△ABC中,∠B=90°,沿AD折叠,使点B落在斜边AC上,若AB=3,BC=4,则BD=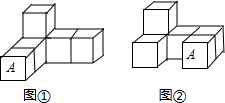 (2012•岳阳)如图,是由6个棱长为1个单位的正方体摆放而成的,将正方体A向右平移2个单位,向后平移1个单位后,所得几何体的视图( )
(2012•岳阳)如图,是由6个棱长为1个单位的正方体摆放而成的,将正方体A向右平移2个单位,向后平移1个单位后,所得几何体的视图( )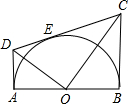 (2012•岳阳)如图,AB为半圆O的直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=
(2012•岳阳)如图,AB为半圆O的直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD= (2012•岳阳)如图,△ABC中,AB=AC,D是AB上的一点,且AD=
(2012•岳阳)如图,△ABC中,AB=AC,D是AB上的一点,且AD=