题目内容
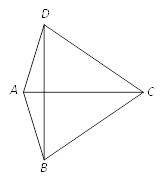
【题目】已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,CD为AB边上中线,E是CB边上的一个动点.
,CD为AB边上中线,E是CB边上的一个动点.
![]() Ⅰ
Ⅰ![]() 求CD的长;
求CD的长;
![]() Ⅱ
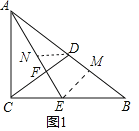
Ⅱ![]() 如图1,连接AE,交CD于点F,当AE平分
如图1,连接AE,交CD于点F,当AE平分![]() 时,求CE,CF的长;
时,求CE,CF的长;
![]() Ⅲ
Ⅲ![]() 如图2,连接DE,将
如图2,连接DE,将![]() 沿DE翻折至
沿DE翻折至![]() ,连接BG,直接写出
,连接BG,直接写出![]() 和
和![]() 间的数量关系.
间的数量关系.

【答案】(1)5;(2)![]() ;(3)
;(3)![]() 若DG在AB的下方,
若DG在AB的下方,![]() 若DG在AB的上方:
若DG在AB的上方:![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 先判断三角形是直角三角形,再根据斜边上的中线等于斜边的一半可求CD的长
先判断三角形是直角三角形,再根据斜边上的中线等于斜边的一半可求CD的长
![]() Ⅱ
Ⅱ![]() 作
作![]() ,根据角平分线的性质可以得
,根据角平分线的性质可以得![]() ,再根据面积法可以求CE的长,取AE中点N,根据中位线定理得
,再根据面积法可以求CE的长,取AE中点N,根据中位线定理得![]() ,
,![]() 再根据平行线分线段成比例,可得
再根据平行线分线段成比例,可得![]() ,代入可得CF的长.
,代入可得CF的长.
![]() Ⅲ
Ⅲ![]() 要分类讨论,DG在AB上方或下方
要分类讨论,DG在AB上方或下方![]() 通过翻折可得
通过翻折可得![]() ,且因为
,且因为![]() ,所以
,所以![]() 可得
可得![]() ,所以D,E,G,B,四点共圆,然后可求数量关系.
,所以D,E,G,B,四点共圆,然后可求数量关系.
解:![]() Ⅰ
Ⅰ![]() ,
,![]() ,
,
![]() ,
,
![]() 是直角三角形,
是直角三角形,![]() ,
,
![]() 是斜边AB上的中线,
是斜边AB上的中线,
![]() ;
;
![]() Ⅱ
Ⅱ![]() 如图1:过点E作
如图1:过点E作![]() 于点M,
于点M,
![]() 平分
平分![]() ,
,![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 取AE中点N,连接DN.
取AE中点N,连接DN.
![]() 为AB中点,N为AE中点,
为AB中点,N为AE中点,
![]() ,且
,且![]() .
.
![]() ,
,
即![]() ,
,
![]() ;
;
![]() Ⅲ
Ⅲ![]() 若DG在AB的下方,如图2
若DG在AB的下方,如图2

![]() .
.
![]() 是
是![]() 翻折得到,
翻折得到,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,E,G,B四点共圆,
,E,G,B四点共圆,
![]() ,
,
![]() ,
,
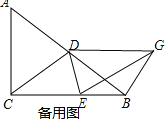
![]() 若DG在AB的上方:如备用图,
若DG在AB的上方:如备用图,
![]() ,
,
![]() ,
,
![]() 是
是![]() 翻折得到,
翻折得到,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,E,G,B四点共圆,
,E,G,B四点共圆,
![]() ,
,
![]() .
.

练习册系列答案
相关题目