��Ŀ����
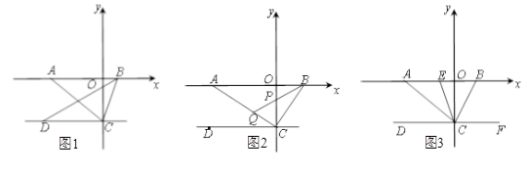
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У��� ![]() Ϊ
Ϊ ![]() �Ḻ������һ�㣬��
�Ḻ������һ�㣬�� ![]() Ϊ
Ϊ ![]() ����������һ�㣬
����������һ�㣬 ![]() ��
�� ![]() ������
������ ![]() ��
�� ![]() �����ϵʽ��
�����ϵʽ�� ![]() ��
�� ![]() .
.
��1��![]() = ��
= �� ![]() = �� ��
= �� �� ![]() �������
�������![]()
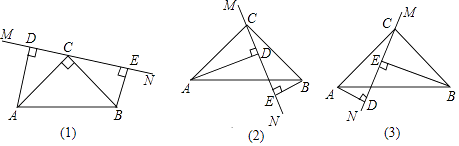
��2����ͼ2���� ![]() ��
�� ![]() ����
���� ![]() �߶�
�߶� ![]() ��һ�㣬����
��һ�㣬���� ![]() ���ӳ�
���ӳ� ![]() ��
�� ![]() �ڵ�
�ڵ� ![]() ������
������ ![]() =��
=�� ![]() ʱ����֤:
ʱ����֤: ![]() ƽ�֡�
ƽ�֡� ![]() ��
��
��3����ͼ3���� ![]() ��
�� ![]() ����
���� ![]() �ǵ�
�ǵ� ![]() ���
��� ![]() ֮��һ���㣬����
֮��һ���㣬���� ![]() ,
, ![]() ʼ��ƽ�֡�
ʼ��ƽ�֡� ![]() ,����
,���� ![]() �ڵ�
�ڵ� ![]() ���
��� ![]() ֮���˶�ʱ��
֮���˶�ʱ�� ![]() ��ֵ�Ƿ�仯�������䣬�����ֵ�����仯����˵������.
��ֵ�Ƿ�仯�������䣬�����ֵ�����仯����˵������.
���𰸡�
��1��-3��-4��6
��2��
�⣺��AC��BC,
���CBQ+��CQP=90��,
�֡ߡ�OBP+��OPB=90��,��OPB=��CPQ,
���CPQ+��OBP=90��,
�֡ߡ�CPQ=��CQP,
���CBQ=��OBP,
��BPƽ�֡�ABC
��3��
�⣺ ![]() ��ֵ�Ƕ�ֵ��
��ֵ�Ƕ�ֵ�� ![]() =2���������£�
=2���������£�
��AC��BC,
���ACB=90��,
���ACD+��BCF=90��,
�֡�CBƽ�֡�ECF,
���ECB=��BCF,
���ACD+��ECB=90��,
�֡ߡ�ACE+��ECB=90��,
���ACD=��ACE,
���DCE=2��ACD,
�֡ߡ�ACD+��ACO=90��,��BCO+��ACO=90��,
���ACD=��BCO,
�֡�C(0,-3)��D(-4,-3),
��CD//AB,
���BEC=��DCE=2��ACD,���BEC=2��BCO,
�� ![]() =2.
=2.
����������1���ɷǸ����������г�������![]()
![]() ,�������a��b��ֵ��������ɵ�DC�ij��Լ�DC���ϵĸߣ����������ε������ʽ������ã���2����AC��BC�ɵá�CBQ+��CQP=90��,�֡�OBP+��OPB=90��,��OPB=��CPQ,��CPQ=��CQP�Ӷ��ɵá�CBQ=��OBP,���ݽ�ƽ���ߵĶ��弴�ɵ�֤��
,�������a��b��ֵ��������ɵ�DC�ij��Լ�DC���ϵĸߣ����������ε������ʽ������ã���2����AC��BC�ɵá�CBQ+��CQP=90��,�֡�OBP+��OPB=90��,��OPB=��CPQ,��CPQ=��CQP�Ӷ��ɵá�CBQ=��OBP,���ݽ�ƽ���ߵĶ��弴�ɵ�֤��
��3����AC��BC,�ɵá�ACB=90�㣬�Ӷ��á�ACD+��BCF=90��,��CBƽ�֡�ECF�ɵá�ECB=��BCF,�֡�ACD+��ECB=90��,��ACE+��ECB=90��,�Ӷ��ɵá�ACD=��ACE,�á�DCE=2��ACD,�Ӷ��ܹ��õ���ACD=��BCO, ����֪�ɵ�CD//AB,�Ӷ��õ�����.
�����㾫����������Ĺؼ���������ǵ�ƽ���ߵ����֪ʶ�����մ�һ���ǵĶ���������һ�����ߣ�������Ƿֳ�������ȵĽǣ��������߽�������ǵ�ƽ���ߣ��Լ��Դ��ߵ����ʵ����⣬�˽ⴹ�ߵ����ʣ�1����һ������ֻ��һ��ֱ���뼺ֱ֪�ߴ�ֱ��2�����߶���̣�