题目内容
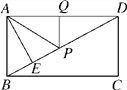
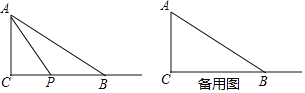
【题目】如图,已知直线y=kx+2![]() 与x轴、y轴分别相交于点A、点B,∠BAO=30°,若将△AOB沿直钱CD折叠,使点A与点B重合,折痕CD与x轴交于点C,与AB交于点D.
与x轴、y轴分别相交于点A、点B,∠BAO=30°,若将△AOB沿直钱CD折叠,使点A与点B重合,折痕CD与x轴交于点C,与AB交于点D.

(1)求k的值;
(2)求点C的坐标;
(3)求直线CD的表达式.
【答案】(1) k=﹣![]() ;(2) 点C(2,0);(3) 直线CD的表达式为:y=
;(2) 点C(2,0);(3) 直线CD的表达式为:y=![]() x﹣2
x﹣2![]() .
.
【解析】
(1)令x=0,则y=2![]() ,即:OB=2
,即:OB=2![]() ,再根据直角三角形中,30°锐角所对的直角边等于斜边的一半解得AB=2OB=4
,再根据直角三角形中,30°锐角所对的直角边等于斜边的一半解得AB=2OB=4![]() ,再根据勾股定理解得:OA=6,从而求得点A坐标,代入解析式即可求解;
,再根据勾股定理解得:OA=6,从而求得点A坐标,代入解析式即可求解;
(2)设:BC=AC=a,则OC=6﹣a,在△BOC中,(2![]() )2+(6﹣a)2=a2,解得:a=4,即可求解;
)2+(6﹣a)2=a2,解得:a=4,即可求解;
(3)点D时AB的中点,则点D(3,![]() ),将点C、D的坐标代入一次函数表达式,即可求解.
),将点C、D的坐标代入一次函数表达式,即可求解.
解:(1)令x=0,则y=2![]() ,即:OB=2
,即:OB=2![]() ,因为∠BAO=30°,所以AB=2OB=4
,因为∠BAO=30°,所以AB=2OB=4![]() ,
,
在Rt△BAO中,由勾股定理得:OA=6,把A(6,0)代入解析式y=kx+2![]() 得:k=﹣
得:k=﹣![]() ;
;
(2)设:BC=AC=a,则OC=6﹣a,
在△BOC中,(2![]() )2+(6﹣a)2=a2,解得:a=4,
)2+(6﹣a)2=a2,解得:a=4,
则点C(2,0);
(3)点D时AB的中点,则点D(3,![]() ),
),
将点C、D的坐标代入一次函数:y=kx+b得: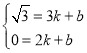 ,解得:
,解得: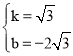 ,
,
故直线CD的表达式为:y=![]() x﹣2
x﹣2![]() .
.

练习册系列答案
相关题目