题目内容
在直角坐标系中,如果⊙O1与⊙O2的半径分别为4和6,点O1、O2的坐标分别为(0,6)、(8,0),则这两个圆的公切线有 条.
【答案】分析:由点O1、O2的坐标分别为(0,6)、(8,0),根据两点间的距离公式即可求得O1O2的长,又由⊙O1与⊙O2的半径分别为4和6,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系,继而求得这两个圆的公切线的条数.
解答:解:∵点O1、O2的坐标分别为(0,6)、(8,0),
∴O1O2=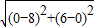 =10,
=10,
∵⊙O1与⊙O2的半径分别为4和6,
又∵4+6=10,
∴⊙O1与⊙O2外切,
∴这两个圆的公切线有3条.
故答案为:3.
点评:此题考查了圆与圆的位置关系以及圆的公切线的知识.此题难度不大,解题的关键是掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系,掌握两圆位置关系与公切线条数的关系.
解答:解:∵点O1、O2的坐标分别为(0,6)、(8,0),
∴O1O2=
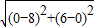 =10,
=10,∵⊙O1与⊙O2的半径分别为4和6,
又∵4+6=10,
∴⊙O1与⊙O2外切,
∴这两个圆的公切线有3条.
故答案为:3.
点评:此题考查了圆与圆的位置关系以及圆的公切线的知识.此题难度不大,解题的关键是掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系,掌握两圆位置关系与公切线条数的关系.

练习册系列答案
相关题目
在直角坐标系中,如果点A在x轴的正半轴上,点B(-1,0)、C(2,4),那么cos∠ABC等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|

 为(
为(