题目内容
【题目】如图,四边形![]() 为一个矩形纸片,
为一个矩形纸片,![]() ,
,![]() ,动点
,动点![]() 自
自![]() 点出发沿
点出发沿![]() 方向运动至
方向运动至![]() 点后停止.
点后停止.![]() 以直线
以直线![]() 为轴翻折,点
为轴翻折,点![]() 落到点
落到点![]() 的位置.设
的位置.设![]() ,
,![]() 与原纸片重叠部分的面积为
与原纸片重叠部分的面积为![]() .
.

(1)当![]() 为何值时,直线
为何值时,直线![]() 过点
过点![]() ?
?
(2)当![]() 为何值时,直线
为何值时,直线![]() 过
过![]() 的中点
的中点![]() ?
?
(3)求出![]() 与
与![]() 的函数关系式.
的函数关系式.
【答案】(1)当x=![]() 时,直线AD1过点C(2)当x=
时,直线AD1过点C(2)当x=![]() 时,直线AD1过BC的中点E(3)当0<x≤2时,y=x;当2<x≤3时,y=
时,直线AD1过BC的中点E(3)当0<x≤2时,y=x;当2<x≤3时,y=![]()
【解析】
试题分析:(1)根据折叠得出AD=AD1=2,PD=PD1=x,∠D=∠AD1P=90°,在Rt△ABC中,根据勾股定理求出AC,在Rt△PCD1中,根据勾股定理得出方程,求出即可;
(2)连接PE,求出BE=CE=1,在Rt△ABE中,根据勾股定理求出AE,求出AD1=AD=2,PD=PD1=x,D1E=![]() ﹣2,PC=3﹣x,在Rt△PD1E和Rt△PCE中,根据勾股定理得出方程,求出即可;
﹣2,PC=3﹣x,在Rt△PD1E和Rt△PCE中,根据勾股定理得出方程,求出即可;
(3)分为两种情况:当0<x≤2时,y=x;当2<x≤3时,点D1在矩形ABCD的外部,PD1交AB于F,求出AF=PF,作PG⊥AB于G,设PF=AF=a,在Rt△PFG中,由勾股定理得出方程(x﹣a)2+22=a2,求出a即可.
试题解析:
(1)
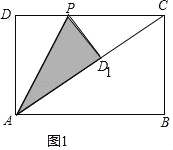
如图1,∵由题意得:△ADP≌△AD1P,
∴AD=AD1=2,PD=PD1=x,∠D=∠AD1P=90°,
∵直线AD1过C,
∴PD1⊥AC,
在Rt△ABC中,AC=![]() ,CD1=
,CD1=![]() ﹣2,
﹣2,
在Rt△PCD1中,PC2=PD12+CD12,
即(3﹣x)2=x2+(![]() ﹣2)2,
﹣2)2,
解得:x=![]() ,
,
∴当x=![]() 时,直线AD1过点C;
时,直线AD1过点C;
(2)如图2,
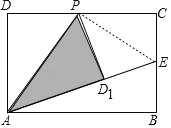
连接PE,
∵E为BC的中点,
∴BE=CE=1,
在Rt△ABE中,AE=![]() =
=![]() ,
,
∵AD1=AD=2,PD=PD1=x,
∴D1E=![]() ﹣2,PC=3﹣x,
﹣2,PC=3﹣x,
在Rt△PD1E和Rt△PCE中,
x2+(![]() ﹣2)2=(3﹣x)2+12,
﹣2)2=(3﹣x)2+12,
解得:x=![]() ,
,
∴当x=![]() 时,直线AD1过BC的中点E;
时,直线AD1过BC的中点E;
(3)如图3,
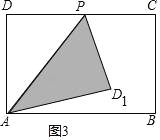
当0<x≤2时,y=x,
如图4,
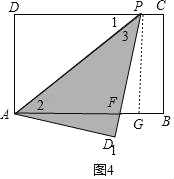
当2<x≤3时,点D1在矩形ABCD的外部,PD1交AB于F,
∵AB∥CD,
∴∠1=∠2,
∵∠1=∠3(根据折叠),
∴∠2=∠3,
∴AF=PF,
作PG⊥AB于G,
设PF=AF=a,
由题意得:AG=DP=x,FG=x﹣a,
在Rt△PFG中,由勾股定理得:(x﹣a)2+22=a2,
解得:a=![]() ,
,
所以y=![]() =
=![]() ,
,
综合上述,当0<x≤2时,y=x;当2<x≤3时,y=![]() .
.

 阅读快车系列答案
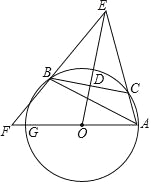
阅读快车系列答案【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.