题目内容
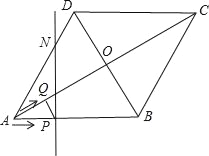
【题目】如图，已知DE∥BC，AO，DF交于点C．∠EAB=∠BCF．
（1）求证：AB∥DF；
（2）求证：OB2=OEOF；
（3）连接OD，若∠OBC=∠ODC，求证：四边形ABCD为菱形．
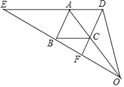
【答案】（1）见解析；（2）见解析;（3）见解析．
【解析】分析：（1）由ED∥BC，
可证得
即可证得AB∥CF；
（2）由平行线分线段成比例定理，即可证得
；
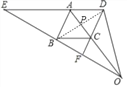
（3）首先作辅助线：连接BD，交AC于点P，易证得
，即可证得
，则得到
，又由
，即可证得四边形ABCD为菱形．
详解：证明：（1）∵DE∥BC，
∴
，
∵
∴
∴AB∥DF．
（2）∵DE∥BC，
∴
∵AB∥CD，
∴
∴
∴
连接BD交AO于点P．
∵DE∥BC，
∴
∵
∴
∵
∴
∴
∴
∵
∴
∵DE∥BC，AB∥DF，
∴四边形ABCD是平行四边形，
∴
∴
∴四边形ABCD是菱形．
练习册系列答案
快捷英语周周练系列答案
相关题目
