题目内容

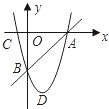
如图，抛物线y=-x2+mx过点A（4，0），O为坐标原点，Q是抛物线的顶点．
（1）求m的值和顶点Q的坐标；
（2）设点P是x轴上方抛物线上的一个动点，过点P作PH⊥x轴，H为垂足，求折线P-H-O长度的最大值．
（1）把点A（4，0）抛物线y=-x2+mx
得，-16+4m=0，
解得m=4，
故此抛物线的解析式为y=-x2+4x．（3分）
Q点坐标为x=-
b
2a
=-
4
2×(-1)
=2，y=
4ac-b2
4a
=
-42
4×(-1)
=4．（6分）

（2）设点P（x，-x2+4x），
则折线P-H-O的长度：l=-x2+5x=-（x-
5
2
）2+
25
4

∴折线P-H-O的长度的最大值为
25
4
．（12分）
练习册系列答案
相关题目
已知：如图，二次函数y=x2+（2k-1）x+k+1的图象与x轴相交于O、A两点．
（1）求这个二次函数的解析式；
（2）在这条抛物线的对称轴右边的图象上有一点B，使锐角△AOB的面积等于3．求点B的坐标；
（3）对于（2）中的点B，在抛物线上是否存在点P，使∠POB=90°？若存在，求出点P的坐标，并求出△POB的面积；若不存在，请说明理由．
如图，抛物线y=x2+bx-c经过直线y=x-3与坐标轴的两个交点A，B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．
（1）求此抛物线的解析式；
（2）点P为抛物线上的一个动点，求使S△APC：S△ACD=5：4的点P的坐标．
设抛物线y=ax2+bx+c与X轴交于两不同的点A（-1，0），B（m，0），（点A在点B的左边），与y轴的交点为点C（0，-2），且∠ACB=90°．
（1）求m的值和该抛物线的解析式；
（2）若点D为该抛物线上的一点，且横坐标为1，点E为过A点的直线y=x+1与该抛物线的另一交点．在X轴上是否存在点P，使得以P、B、D为顶点的三角形与△AEB相似？若存在，求出点P的坐标；若不存在，请说明理由．
（3）连接AC、BC，矩形FGHQ的一边FG在线段AB上，顶点H、Q分别在线段AC、BC上，若设F点坐标为（t，0），矩形FGHQ的面积为S，当S取最大值时，连接FH并延长至点M，使HM=k•FH，若点M不在该抛物线上，求k的取值范围．
如图一次函数图象与x轴y轴交于A（6，0）B（0，2
3
）线段AB的垂直平分线交x轴于点C交y轴于点D
求：（1）求这个一次函数的解析式；
（2）过A，B，C三点的抛物线解析式．
某市人民广场上要建造一个圆形的喷水池，并在水池中央垂直安装一个柱子OP，柱子顶端P处装上喷头，由P处向外喷出的水流（在各个方向上）沿形状相同的抛物线路径落下（如图所示）．若已知OP=3米，喷出的水流的最高点A距水平面的高度是4米，离柱子OP的距离为1米．
（1）求这条抛物线的解析式；
（2）若不计其它因素，水池的半径至少要多少米，才能使喷出的水流不至于落在池外？
蔬菜基地种植的某种蔬菜，根据今年的市场行情，预计从3月1日起的50天内，它的市场售价y1（万元）与上市时间x的关系可用图（1）中的一条折线表示；他的种植成本y2（万元）与上市时间x的关系可用力（2）中的抛物线的一部分来表示．若市场售价减去种植成本为纯利润

（1）求y1、y2关于x的函数关系式；
（2）哪天上市这种绿色蔬菜既不赔本也不赚钱？
（3）哪天上市的蔬菜的利润最大？
二次函数y=ax2+bx+c（b、c为常数）．
（1）若二次函数的图象经过A（-2，-3）和B（2，5）两点，求此二次函数的关系式；
（2）求此二次函数图象的顶点坐标及对称轴．
如图中是抛物线形拱桥，当水面在n时，拱顶离水面2m，水面宽4m，水面下降1m，水面宽度增加多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网