题目内容
已知等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于O,∠ABD=30°,AC⊥BC,AB=8cm,则△COD的面积为
- A.
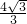 cm2
cm2 - B.
 cm2
cm2 - C.
 cm2
cm2 - D.
 cm2
cm2
A
分析:由已知∠ABD=30°,可得∠CAB=30°,又因为AC⊥BC,根据直角三角形中30度所对的角是斜边的一半可求得BC,AC,的长;进而求出三角形ACB的面积,再求出三角形COB的面积,所以求出三角形AOB的面积,又因为AB∥CD所以△AOB∽△DOC,利用相似的性质:面积之比等于相似比的平方即可求出△COD的面积.
解答:∵梯形ABCD是等腰梯形,CD∥AB,
由SAS可证△DAB≌△CBA,
∴∠CAB=∠DCA=30°,
∵∠CAB=30°,又因为AC⊥BC,
∴∠DAB=∠CBA=60°,
∴∠DAC=∠DCA=30°,
∴CD=AD=BC=4cm,
∴AC2=AB2-BC2,
∴AC=4 cm,
cm,
∵梯形ABCD是等腰梯形,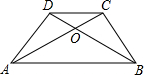
∴AC=BD=4 cm,
cm,
∴S△ABC= ×4×4
×4×4 =8
=8 cm,
cm,
设DO为x,则CO=x,则AO=BO=(4 -x)cm,
-x)cm,
在Rt△COB中,CO2+BC2=BO2,
即:x2+42=(4 -x)2
-x)2
∴D0=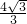 cm,
cm,
∴S△ADO= ×
×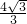 ×4=
×4=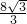 ,
,
∴S△AOB=S△ABC-S△ADO=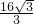
∵AB∥CD,
∴△AOB∽△DOC,
∴(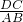 )2=
)2=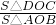
∴S△DOC=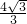 ,
,
故选A.
点评:此题主要考查等腰梯形的性质:①等腰梯形是轴对称图形,它的对称轴是经过上下底的中点的直线;②等腰梯形同一底上的两个角相等;③等腰梯形两条对角线相等.
分析:由已知∠ABD=30°,可得∠CAB=30°,又因为AC⊥BC,根据直角三角形中30度所对的角是斜边的一半可求得BC,AC,的长;进而求出三角形ACB的面积,再求出三角形COB的面积,所以求出三角形AOB的面积,又因为AB∥CD所以△AOB∽△DOC,利用相似的性质:面积之比等于相似比的平方即可求出△COD的面积.
解答:∵梯形ABCD是等腰梯形,CD∥AB,
由SAS可证△DAB≌△CBA,
∴∠CAB=∠DCA=30°,
∵∠CAB=30°,又因为AC⊥BC,
∴∠DAB=∠CBA=60°,
∴∠DAC=∠DCA=30°,
∴CD=AD=BC=4cm,
∴AC2=AB2-BC2,
∴AC=4
 cm,
cm,∵梯形ABCD是等腰梯形,

∴AC=BD=4
 cm,
cm,∴S△ABC=
 ×4×4
×4×4 =8
=8 cm,
cm,设DO为x,则CO=x,则AO=BO=(4
 -x)cm,
-x)cm,在Rt△COB中,CO2+BC2=BO2,
即:x2+42=(4
 -x)2
-x)2∴D0=
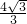 cm,
cm,∴S△ADO=
 ×
×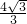 ×4=
×4=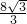 ,
,∴S△AOB=S△ABC-S△ADO=
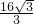
∵AB∥CD,
∴△AOB∽△DOC,
∴(
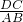 )2=
)2=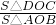
∴S△DOC=
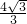 ,
,故选A.
点评:此题主要考查等腰梯形的性质:①等腰梯形是轴对称图形,它的对称轴是经过上下底的中点的直线;②等腰梯形同一底上的两个角相等;③等腰梯形两条对角线相等.

练习册系列答案
相关题目
 3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( )
3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( )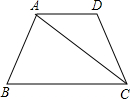 如图,已知等腰梯形ABCD的周长是20,AD∥BC,AD<BC,∠BAD=120°,对角线AC平分∠BCD,则S梯形ABCD=
如图,已知等腰梯形ABCD的周长是20,AD∥BC,AD<BC,∠BAD=120°,对角线AC平分∠BCD,则S梯形ABCD= 23、如图所示,已知等腰梯形ABCD中,AD∥BC,AB=CD,点E为梯形外一点,且AE=DE.
23、如图所示,已知等腰梯形ABCD中,AD∥BC,AB=CD,点E为梯形外一点,且AE=DE.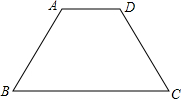 如图,已知等腰梯形ABCD中,AB=CD,AD=
如图,已知等腰梯形ABCD中,AB=CD,AD=