题目内容
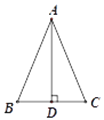
【题目】已知△ABC中，点D为BC的中点，BD=
AB，AD⊥BC．
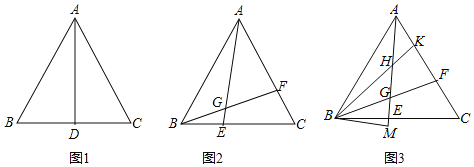
（1）如图1，求∠BAD的度数；
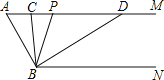
（2）如图2，点E为BC上一点，点F为AC上一点，连接AE、BF交于点G，若∠AGF=60°，求证：BE=CF；
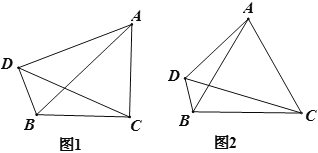
（3）如图3，在（2）的条件下，点G为BF的中点，点H为AG上一点，延长BH交AC于点K，AK=HK，BM⊥AE交AE延长线于点M，BG=9，HM=10，求线段AG的长．
【答案】（1）30°；（2）证明见解析；（3）14.5
【解析】
（1）先判断出AB=AC，可得△ABC是等边三角形，根据等边三角形三线合一的性质可得结论；
（2）利用等式的性质判断出∠BAE=∠BCF，进而得出△ABE≌△BCF，即可得出结论；
（3）如图3，作辅助线，构建矩形NMDF，先根据三角形的中位线可得DM=FN=
，由△ANF≌△HMB，得AN=HM=10，计算NG的长，相加可得结论．
（1）∵点D为BC的中点，AD⊥BC，
∴AB=AC，BD=CD=
BC，
∵BD=AB，
∴AB=BC=AC，
∴△ABC是等边三角形，
∴∠BAC=60°，
∵AD⊥BC，
∴∠BAD=∠BAC=30°；
（2）由（1）知，△ABC是等边三角形，
∴AB=BC，∠ABC=∠C=60°，
∴∠ABF+∠CBF=60°，
∵∠AGF=60°，
∴∠BAE+∠ABF=60°，
∴∠BAE=∠CBF，
在△ABE和△BCF中，
，
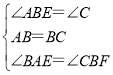∴△ABE≌△BCF（ASA），
∴BE=CF，
（3）如图，过F作FN⊥AE于N，过F作FD⊥BM，交BM的延长线于D，
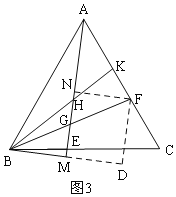
∵AM⊥BM，
∴GM∥DF，
∵BG=GF，
∴BM=DM，
∵∠AGF=60°，
∴∠BGM=60°，
∵BM⊥AE，
∴∠BMG=90°，
∴∠GBM=30°，
在Rt△BMG中，MG=BG=
，BM=DM=FN=，
∵AK=HK，
∴∠HAK=∠AHK=∠BHM，
∵∠ANF=∠HMB=90°，
∴△ANF≌△HMB，
∴AN=HM=10，
Rt△FGN中，∠NFG=∠GBM=30°，
∴GN=GF=，
∴AG=AN+NG=10+=14.5．
即：AG的长为14.5．
