题目内容
某同学在做练习时,遇到这样一道题:“当a=![]() ,b=-1时,求多项式3a3+4a2b-3b3与-3a3-4a2b+2b3+1的和.”做完后,他指出题中所给的a的值是多余的,你认为他的说法有道理吗?
,b=-1时,求多项式3a3+4a2b-3b3与-3a3-4a2b+2b3+1的和.”做完后,他指出题中所给的a的值是多余的,你认为他的说法有道理吗?
答案:
解析:
提示:
解析:
|
解:(3a3+4a2b-3b3)+(-3a3-4a2b+2b3+1) =(3a3-3a3)+(4a2b-4a2b)+(-3b3+2b3)+1=-b3+1 当b=-1时,原式=2,∵-b3+1中不含字母a,∴与a值无关. |
提示:
|
要想得出结论,应先把两个多项式的和求出来,若结果中不含有字母a,则与字母a的值无关,该同学的说法有道理. |

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
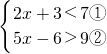 .小虎解法:由不等式①,得x<2由不等式②,得x>3
.小虎解法:由不等式①,得x<2由不等式②,得x>3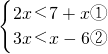 .小虎解法:②-①,得不等式组的解集为x<-13.
.小虎解法:②-①,得不等式组的解集为x<-13. 时,求代数式1-(3xy+x)+[-(2x-3yx)]的值”.做完后,他指出题中所给的y值是多余的,你认为他的说法正确吗?为什么?
时,求代数式1-(3xy+x)+[-(2x-3yx)]的值”.做完后,他指出题中所给的y值是多余的,你认为他的说法正确吗?为什么?