题目内容
【题目】如图,已知在△ABC中,AB=AC=6,BC=10.求△ABC的外接圆的半径r.
【答案】![]()
【解析】
连接AO交BC于D,连接OB、OC.已知AB=AC,由同圆或等圆中,等弦对等弧可得圆弧AB=圆弧AC,由此可得∠BOA=∠AOC;
在△BOC中,OB=OC,∠BOD=∠COD,根据三线合一可得OA⊥BC,BD=DC,根据直角三角形勾股定理,即可求得AD;
设CO=R,则DO=AOAD=R![]() ,在Rt△CDO中,由勾股定理就可以得出关于R的方程,求出R的值即可解答本题.
,在Rt△CDO中,由勾股定理就可以得出关于R的方程,求出R的值即可解答本题.
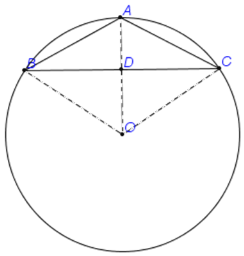
连接AO交BC于D,连接OB、OC
∵ AB=AC
∴弧AB=弧AC(同圆或等圆中,等弦对等弧)
∴ ∠BOA=∠AOC (同圆或等圆中,等弧所对的圆心角相等)
∵ OB=OC ∠BOA=∠AOC
∴ OA⊥BC (三线合一)
BD=DC=![]() ×BC=
×BC=![]() ×10=5(三线合一)
×10=5(三线合一)
∴AD=![]() =
=![]() =
=![]() (直角三角形勾股定理求值)
(直角三角形勾股定理求值)
设CO=R 则DO=AOAD=R![]()
∵ △CDO是直角三角形
∴![]() +
+![]() =
=![]() (直角三角形勾股定理)
(直角三角形勾股定理)
∵DO=R![]() CO=R DC=5
CO=R DC=5
∴![]() +
+![]() =
=![]()
解得R=![]()
所以△ABC的外接圆的半径R为![]()

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
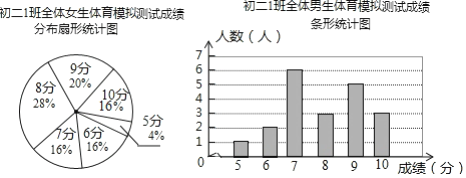
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | |
男生 | ________ | 2 | 8 | 7 |
女生 | 7.92 | 1.99 | 8 | ________ |
根据以上信息,解答下列问题:
(1)这个班共有男生________人,共有女生________人;
(2)补全初二1班体育模拟测试成绩分析表;
(3)你认为在这次体育测试中,1班的男生队、女生队哪个表现更突出一些?并写出一条支持你的看法的理由.