题目内容
如图，已知AB∥CD，CE、AE分别平分∠ACD、∠CAB，则∠AEC=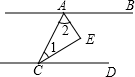
90
90
°．分析：先根据平行线的性质得出∠BAC++DCA的度数，再由角平分线的定义得出∠1+∠2的度数，根据三角形内角和定理即可得出结论．
解答：解：∵AB∥CD，
∴∠BAC++DCA=180°，
∵CE、AE分别平分∠ACD、∠CAB，
∴∠1+∠2=
（∠BAC++DCA）=
×180°=90°，
在△ACE中，
∵∠1+∠2=90°，
∴∠AEC=180°-（∠1+∠2）=180°-90°=90°．
故答案为；90．
∴∠BAC++DCA=180°，
∵CE、AE分别平分∠ACD、∠CAB，
∴∠1+∠2=
| 1 |
| 2 |
| 1 |
| 2 |
在△ACE中，
∵∠1+∠2=90°，
∴∠AEC=180°-（∠1+∠2）=180°-90°=90°．
故答案为；90．
点评：本题考查的是平行线的性质，在解答此类题目时往往用到三角形的内角和是180°这一关键条件．
练习册系列答案
相关题目
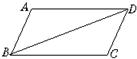15、如图，已知AB=CD且∠ABD=∠BDC，要证∠A=∠C，判定△ABD≌△CDB的方法是（ ）
如图，已知AB∥CD，∠1=50°25′，则∠2的大小是
如图，已知 AB∥CD，∠A=53°，则∠1的度数是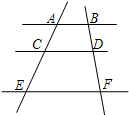
如图，已知AB∥CD∥EF，那么下列结论中，正确的是（ ）