题目内容
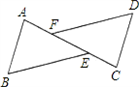
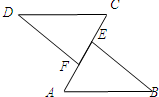17、已知CD∥AB，DF∥EB，DF=EB，问AF=CE吗？说明理由．分析：首先根据AAS证明△DFC≌△BEA，由全等三角形的对应边相等得出AE=CF，然后根据等式的性质得出AF=CE．
解答：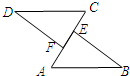
解：AF=CE．理由如下：
∵CD∥AB，∴∠C=∠A，
∵DF∥EB，∴∠DFC=∠BEA，
在△DFC和△BEA中，
∵∠C=∠A，∠DFC=∠BEA，DF=EB，
∴△DFC≌△BEA（AAS），
∴AE=CF，
∴AE-EF=CF-EF，
∴AF=CE．
解：AF=CE．理由如下：∵CD∥AB，∴∠C=∠A，
∵DF∥EB，∴∠DFC=∠BEA，
在△DFC和△BEA中，
∵∠C=∠A，∠DFC=∠BEA，DF=EB，
∴△DFC≌△BEA（AAS），
∴AE=CF，
∴AE-EF=CF-EF，
∴AF=CE．
点评：本题主要考查了全等三角形的判定与性质，根据AAS证明△DFC≌△BEA是解题的关键．
练习册系列答案
相关题目
如图，已知CD是AB的中垂线，垂足为点D，DE⊥AC于点E，DF⊥BC于点F．
如图所示，已知CD⊥DA，DA⊥AB，∠1=∠2．
