题目内容
如图，△COD是△AOB绕点O顺时针方向旋转40°后所得的图形，点C恰好在AB上，∠AOD＝90°，则∠B的度数是（ ）
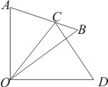
| A．500 | B．400 | C．450 | D．600 |
D
已知△COD是△AOB绕点O顺时针方向旋转40°后所得的图形，可得△COD≌△AOB，旋转角为40°，∵点C恰好在AB上，∴△AOC为等腰三角形，可结合三角形的内角和定理求∠B的度数．
解：根据旋转性质得△COD≌△AOB，
∴CO=AO，
由旋转角为40°，
可得∠AOC=∠BOD=40°，
∴∠OAC=（180°-∠AOC）÷2=70°，
∠BOC=∠AOD-∠AOC-∠BOD=10°，
∠AOB=∠AOC+∠BOC=50°，
在△AOB中，由内角和定理得∠B=180°-∠OAC-∠AOB=180°-70°-50°=60°．
故答案选Ｄ．
解：根据旋转性质得△COD≌△AOB，
∴CO=AO，
由旋转角为40°，
可得∠AOC=∠BOD=40°，
∴∠OAC=（180°-∠AOC）÷2=70°，
∠BOC=∠AOD-∠AOC-∠BOD=10°，
∠AOB=∠AOC+∠BOC=50°，
在△AOB中，由内角和定理得∠B=180°-∠OAC-∠AOB=180°-70°-50°=60°．
故答案选Ｄ．
练习册系列答案
相关题目
沿直线
向右平移3cm，得 到
,则线段
cm
)cm2
