题目内容
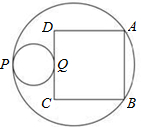15、如图，PQ=3，以PQ为直径的圆与一个以5为半径的圆相切于点P，正方形ABCD的顶点A、B在大圆上，小圆在正方形的外部且与CD切于点Q．则AB=6
．分析：连接MA，MP，延长PQM与AB交于E，构建直角三角形，解出直角三角形即可．
解答：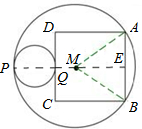
解：设大圆的圆心为M点，连接MA，MP，延长PQM与AB交于E；
设AB=2a（正方形的边长），在直角三角形MAE中，
∵小圆在正方形的外部且与CD切于点Q．
∴PQ⊥CD，
∵CD∥AB，
∴PE⊥AB，
∴AE=BE，
∴AM2=ME2+AE2，
即52=（2a-2）2+a2
解得，a=3或-1.4（舍去）
所以AB=6．
解：设大圆的圆心为M点，连接MA，MP，延长PQM与AB交于E；设AB=2a（正方形的边长），在直角三角形MAE中，
∵小圆在正方形的外部且与CD切于点Q．
∴PQ⊥CD，
∵CD∥AB，
∴PE⊥AB，
∴AE=BE，
∴AM2=ME2+AE2，
即52=（2a-2）2+a2
解得，a=3或-1.4（舍去）
所以AB=6．
点评：解决本题的难点是做出辅助线构造直角三角形．
练习册系列答案
相关题目
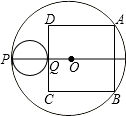如图，PQ=10，以PQ为直径的圆与一个以20为半径的⊙O内切于点P，与正方形ABCD切于点Q，其中A、B两点在⊙O上．若AB=
如图，PQ=10，以PQ为直径的圆与一个以20为半径的⊙O内切于点P，与正方形ABCD切于点Q，其中A、B两点在⊙O上．若AB=m+
