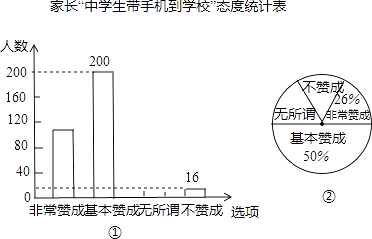
题目内容
【题目】如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是 . 
【答案】42
【解析】方法一: 解:连接CE,
因为BD:CD=2:1,所以△BDE和△CDE的面积之比为2:1,
又因为DE∥AC,
∴ ![]() =
= ![]() ,
,
∴S△BDE:S△ABC=4:9,
又因为△ABC的面积是63,
∴△BDE的面积为:28,
所以△CDE的面积为14,
因为FE:ED=2:1,所以△FDC和△CDE的面积之比为3:1
所以答案是:42.
方法二:解:作MW⊥BC,AN⊥BC,垂足分别为W,N.
∵BD:CD=2:1,DE∥AC,
∴BE:AE=2:1,
∴BD:BC=DE:AC=BE:AB=2:3,
∴S△BDE:S△ABC=4:9,
∴S△BDE= ![]() ×63=28,
×63=28,
∵FE:ED=2:1=4:2,
∴EF:AC=4:3,
∴S△MEF:S△AMC=16:9,
∴EM:AM=4:3,
假设EM=4x,AM=3x,BE= ![]() AB=2AE=2(EM+AM)=14x,
AB=2AE=2(EM+AM)=14x,
∴BM:AM=18x:3x=18:3,
∴MW:AN=BM:AB=18:21=6:7,
∴S△BMC:S△ABC= ![]() BCWM:
BCWM: ![]() BCAN=WM:AN=6:7,
BCAN=WM:AN=6:7,
∵S△ABC=63,
∴S△BMC=54,
∴S△AMC=63﹣54=9,
∵S△MEF:S△AMC=16:9,
∴S△MEF=16,
∵S△BDE= ![]() ×63=28,
×63=28,
∴S四边形MEDC=63﹣9﹣28=26,
∴△CDF的面积是:26+16=42.
所以答案是:42.
【考点精析】关于本题考查的三角形的面积和平行线分线段成比例,需要了解三角形的面积=1/2×底×高;三条平行线截两条直线,所得的对应线段成比例才能得出正确答案.