Question

【题目】如图，菱形ABCD的周长为20，对角线AC长为，点E、F分别为AC、BC边上的动点．

（1）直接写出菱形ABCD的面积：_______；

（2）直接写出BE+EF的最小值_______；并在图中作出此时的点E和点F．

Answer 1

【答案】（1）20；（2）2，E、F两点的位置见解析．

【解析】

(1)如图：连接BD交AC于O点,再根据菱形的性质求出AB和OA的长,再利用勾股定理求得OB的长,进而求得BD的长,最后利用菱形的面积等于对角线积的一半解答即可；

（2）根据点到直线的距离垂线段最短，可确定当点E与点O重合时BE最短；当F与B重合时EF=OB取最小值，即 BE+EF=2OB=BD的长．

（1）解：连接BD交AC于O点,

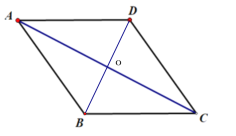
∵菱形ABCD的周长为20，对角线AC=

∴AB=5,OA=

∴OB==

∴BD=2

∴菱形的面积为: =20．

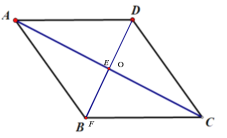
（2）解：当点E与点O重合时BE最短，BE=OB（垂线段最短）；

当F与B重合时，EF=OB取最小值；

所以BE+EF=2OB=BD=2；

E、F的位置如图所示．