Question

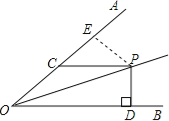
【题目】如图，∠AOB=30°，OP平分∠AOB，PD⊥OB于D，PC∥OB交OA于C，若PC=10，则PD= ．

Answer 1

【答案】5

【解析】试题分析：根据角平分线的定义和平行线的性质得到∠COP=∠CPO=∠BOP，即可得出PC=OC，根据角平分线的性质得出PD=PE，求出PE，即可求出PD．

解：∵OP平分∠AOB，

∴∠AOP=∠BOP，

∵PC∥OB，

∴∠CPO=∠BOP，∴∠CPO=∠AOP，

∴PC=OC，

∵PC=10，

∴OC=PC=10，

过P作PE⊥OA于点E，

∵PD⊥OB，OP平分∠AOB，

∴PD=PE，

∵PC∥OB，∠AOB=30°

∴∠ECP=∠AOB=30°

在Rt△ECP中，PE=PC=5，

∴PD=PE=5，

故答案为：5．