��Ŀ����
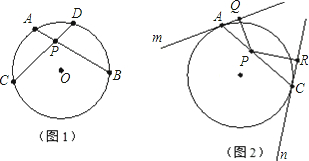
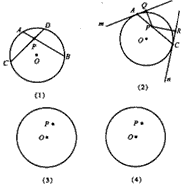
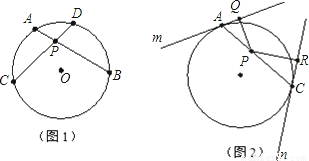
���Ķ����в��ϣ�Բ�ڵ������ཻ�ң�������ֳɵ������߶γ��Ļ���ȣ�����ͼ1������AB��CD���ڵ�P����PA•PB=PC•PD������������ϲ��ϣ�����������⣮
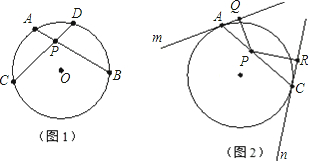
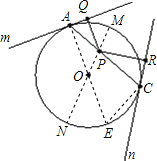
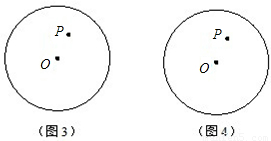
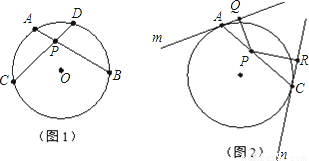
��֪��O�İ뾶Ϊ2��P�ǡ�O��һ�㣬��OP=1������P����-��AC����A��C����ֱ�����O������m��n����PQ��m�ڵ�Q��PR��n�ڵ�R������ͼ2��
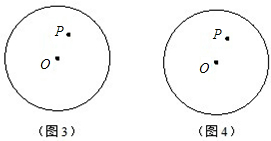
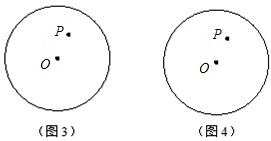
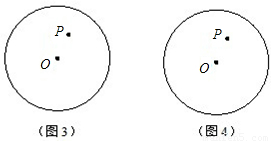
��1����ACǡ����Բ��O��������ͼ3�л������������ͼ�Σ������㣺
| 1 |
| PQ |
| 1 |
| PR |
��2����OP��AC��������ͼ4�л������������ͼ�Σ������㣺
| 1 |
| PQ |
| 1 |
| PR |
��3����AC�ǹ���P����һ�ң�ͼ2���������ϣ�1����2���Ľ��ۣ����룺
| 1 |
| PQ |
| 1 |
| PR |
��������1������AC��Բ�ģ���ôQ��A�غϣ�R��C�غϣ��ɸ���OP�Ͱ뾶�ij����PA��PC�ij�����PQ��PR�ij����ɴ˿ɵó�����Ľ��ۣ�
��2������OA�����ѵó�OA��PQ����ô�ɵó���OAP=��APQ��������ֱ��������OAP�У������OAP�Ķ�����AP�ij�����������ֱ��������APQ�����PQ�ij���ͬ�������PR�ij��������������Ľ��ۣ��������ͨ��֤��ADP�͡�PAQ���ƣ��ó�
��ֵ��ͬ��������CD�ó�
��ֵ��
��3������Ҫͨ����������������⣮����A��ֱ������O�ڵ�E������EC��ͨ�����������Ρ�AEC�ס�PAQ���ó�����AC��PQ��AE��AP�ı�����ϵʽ��ͬ�������AC��PR��AE��PC�ı�����ϵʽ����ʽ�����ɵó�
+
�ı���ʽ��Ȼ������ཻ�Ҷ�������֤������Ľ��ۣ�
���ڶ���֤���ͣ�2���ĵڶ�������ȫ��ͬ����
��2������OA�����ѵó�OA��PQ����ô�ɵó���OAP=��APQ��������ֱ��������OAP�У������OAP�Ķ�����AP�ij�����������ֱ��������APQ�����PQ�ij���ͬ�������PR�ij��������������Ľ��ۣ��������ͨ��֤��ADP�͡�PAQ���ƣ��ó�
| 1 |
| PQ |
| 1 |
| PR |
��3������Ҫͨ����������������⣮����A��ֱ������O�ڵ�E������EC��ͨ�����������Ρ�AEC�ס�PAQ���ó�����AC��PQ��AE��AP�ı�����ϵʽ��ͬ�������AC��PR��AE��PC�ı�����ϵʽ����ʽ�����ɵó�
| 1 |
| PQ |
| 1 |
| PR |
���ڶ���֤���ͣ�2���ĵڶ�������ȫ��ͬ����
���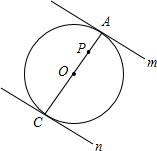 �⣺��1��AC��Բ��O����m��n�ֱ��С�O�ڵ�A��C��
�⣺��1��AC��Բ��O����m��n�ֱ��С�O�ڵ�A��C��
��AC��m�ڵ�A��AC��n�ڵ�C��
��PQ��m�ڵ�Q��PR��n�ڵ�R��
��Q��A�غϣ�R��C�غϣ�
��OP=1��AC=4��
��PQ=1��PR=3��
��
+
=1+
=
��
��2������OA��
��OP��AC�ڵ�P����OP=1��OA=2��
���OAP=30�㣮
��AP=
��
��OA��ֱ��m��PQ��Fֱ��m��
��OA��PQ����PQA=90�㣮
���APQ=��OAP=30�㣮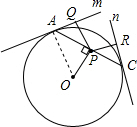
��Rt��AQP��PQ=
��ͬ����PR=
��
��
+
=
+
=
��
��3������
+
=
��
֤��������A��ֱ������O�ڵ�E������EC��
���ECA=90�㣮
��AE��ֱ��m��PQ��ֱ�ߣ�
��AE��PQ�ҡ�PQA=90�㣮
���EAC=��APQ��
���AEC�ס�PAQ��
��
=
��
ͬ���ɵã�
=
��
��+�ڣ��ã�
+
=
+
��
+
=
��
+
��
=
•
=
��
��P��ֱ������O��M��N��
�����Ķ����Ͽ�֪��AP•PC=PM•PN=3��
��
+
=
��
 �⣺��1��AC��Բ��O����m��n�ֱ��С�O�ڵ�A��C��
�⣺��1��AC��Բ��O����m��n�ֱ��С�O�ڵ�A��C����AC��m�ڵ�A��AC��n�ڵ�C��
��PQ��m�ڵ�Q��PR��n�ڵ�R��
��Q��A�غϣ�R��C�غϣ�
��OP=1��AC=4��
��PQ=1��PR=3��
��
| 1 |
| PQ |
| 1 |
| PR |
| 1 |
| 3 |
| 4 |
| 3 |
��2������OA��
��OP��AC�ڵ�P����OP=1��OA=2��
���OAP=30�㣮
��AP=
| 3 |
��OA��ֱ��m��PQ��Fֱ��m��
��OA��PQ����PQA=90�㣮
���APQ=��OAP=30�㣮

��Rt��AQP��PQ=
| 3 |
| 2 |
| 3 |
| 2 |
��
| 1 |
| PQ |
| 1 |
| PR |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
��3������
| 1 |
| PQ |
| 1 |
| PR |
| 4 |
| 3 |
֤��������A��ֱ������O�ڵ�E������EC��
���ECA=90�㣮
��AE��ֱ��m��PQ��ֱ�ߣ�
��AE��PQ�ҡ�PQA=90�㣮
���EAC=��APQ��
���AEC�ס�PAQ��
��
| AC |
| PQ |
| AE |
| AP |
ͬ���ɵã�
| AC |
| PR |
| AE |
| PC |
��+�ڣ��ã�
| AC |
| PQ |
| AC |
| PR |
| AE |
| AP |
| AE |
| PC |

��
| 1 |
| PQ |
| 1 |
| PR |
| AE |
| AC |
| 1 |
| AP |
| 1 |
| PC |
=
| AE |
| AC |
| PC+AP |
| AP•PC |
| AE |
| AP•PC |
��P��ֱ������O��M��N��
�����Ķ����Ͽ�֪��AP•PC=PM•PN=3��
��
| 1 |
| PQ |
| 1 |
| PR |
| 4 |
| 3 |
������������Ҫ���������������κ��ཻ�Ҷ�����Ӧ�ã��������������εó���������ص��߶γɱ����ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
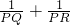 ��ֵ��
��ֵ��
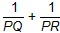 ��ֵ��
��ֵ��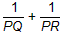 ��ֵ��
��ֵ��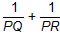 ��ֵ��������֤����
��ֵ��������֤����
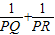 ��ֵ��
��ֵ��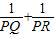 ��ֵ��
��ֵ��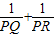 ��ֵ��������֤����
��ֵ��������֤����
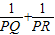 ��ֵ��
��ֵ��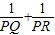 ��ֵ��
��ֵ��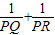 ��ֵ��������֤����
��ֵ��������֤����