题目内容
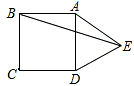 如图所示,以正方形ABCD中AD边为一边向外作等边△ADE,则∠AEB=
如图所示,以正方形ABCD中AD边为一边向外作等边△ADE,则∠AEB=
- A.10°
- B.15°
- C.20°
- D.12.5°
B
分析:根据正方形性质求出AB=AD,∠BAD=90°,根据等边三角形的性质得出∠EAD=60°,AD=AE=AB,推出∠ABE=∠AEB,根据三角形的内角和定理求出即可.
解答:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵三角形ADE是等边三角形,
∴∠EAD=60°,AD=AE=AB,
∴∠ABE=∠AEB,
∵∠ABE+∠AEB+∠BAE=180°,
∴∠AEB= ×(180°-90°-60°)=15°,
×(180°-90°-60°)=15°,
故选B.
点评:本题考查了等腰三角形的性质,三角形的内角和定理,正方形性质,等边三角形的性质的应用,关键是求出∠BAE的度数,通过做此题培养了学生的推理能力,题目综合性比较强,是一道比较好的题目.
分析:根据正方形性质求出AB=AD,∠BAD=90°,根据等边三角形的性质得出∠EAD=60°,AD=AE=AB,推出∠ABE=∠AEB,根据三角形的内角和定理求出即可.
解答:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵三角形ADE是等边三角形,
∴∠EAD=60°,AD=AE=AB,
∴∠ABE=∠AEB,
∵∠ABE+∠AEB+∠BAE=180°,
∴∠AEB=
 ×(180°-90°-60°)=15°,
×(180°-90°-60°)=15°,故选B.
点评:本题考查了等腰三角形的性质,三角形的内角和定理,正方形性质,等边三角形的性质的应用,关键是求出∠BAE的度数,通过做此题培养了学生的推理能力,题目综合性比较强,是一道比较好的题目.

练习册系列答案
相关题目
 B的延长线于点F,BF=4.
B的延长线于点F,BF=4.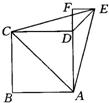 16、如图所示,以正方形ABCD的对角线AC为边作等边三角形ACE,过点E作EF⊥AD,交AD的延长线于F,则∠DEF=
16、如图所示,以正方形ABCD的对角线AC为边作等边三角形ACE,过点E作EF⊥AD,交AD的延长线于F,则∠DEF=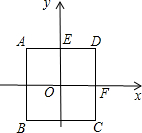 如图所示,以正方形ABCD平行于边的对称轴为坐标轴建立直角坐标系,若正方形的边长为4.
如图所示,以正方形ABCD平行于边的对称轴为坐标轴建立直角坐标系,若正方形的边长为4.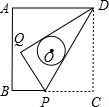 已知正方形ABCD的边长为2,点P是BC上的一点,将△DCP沿DP折叠至△DPQ,若DQ,DP恰好与如图所示的以正方形ABCD的中心O为圆心的⊙O相切,则折痕DP的长为( )
已知正方形ABCD的边长为2,点P是BC上的一点,将△DCP沿DP折叠至△DPQ,若DQ,DP恰好与如图所示的以正方形ABCD的中心O为圆心的⊙O相切,则折痕DP的长为( )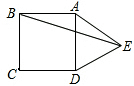 如图所示,以正方形ABCD中AD边为一边向外作等边△ADE,则∠AEB=( )
如图所示,以正方形ABCD中AD边为一边向外作等边△ADE,则∠AEB=( )