题目内容
如图所示，以正方形ABCD的边AB为直径，在正方形内部作半圆，圆心为O，DF切半圆于E，交A
B的延长线于点F，BF=4．（1）求证：△EFO∽△AFD，并求
| FE | FA |
（2）求cos∠F的值；
（3）求线段BE的长．
分析：（1）先证明△EFO∽△AFD，然后根据相似三角形的对应边成比例得到
=
；
（2）解答此题的关键是由△OEF∽△DAF得出AF=2EF，再根据此数值求出EF和FO，然后即可求出cos∠F；
（3）由△BEF∽△EAF，设BE=k，则AE=2k，即可求得BE．
| EF |
| AF |
| EO |
| AD |
（2）解答此题的关键是由△OEF∽△DAF得出AF=2EF，再根据此数值求出EF和FO，然后即可求出cos∠F；
（3）由△BEF∽△EAF，设BE=k，则AE=2k，即可求得BE．
解答：解：（1）易知∠OEF=∠FAD=90°，而∠F=∠F，
故△EFO∽△AFD，
所以
=
，
而EO=AO=
AB=
AD，即
=
；
（2）由△OEF∽△DAF，得
=
=
=
，
即AF=2EF，又EF2=FB•FA=BF•2EF，
∴EF=2BF=8，AF=2EF=16，
∴AB=AF-BF=12，
FO=
AB+BF=10．
cos∠F=
=
；
（3）由△BEF∽△EAF，得
=
=
=
，
设BE=k，则AE=2k，
由AE2+BE2=AB2，得
（2k）2+k2=122，
解得k=
，
故BE=
．
故△EFO∽△AFD，
所以
| EF |
| AF |
| EO |
| AD |
而EO=AO=
| 1 |
| 2 |
| 1 |
| 2 |
| FE |
| FA |
| 1 |
| 2 |
（2）由△OEF∽△DAF，得
| EF |
| AF |
| OE |
| DA |
| OE |
| AB |
| 1 |
| 2 |
即AF=2EF，又EF2=FB•FA=BF•2EF，
∴EF=2BF=8，AF=2EF=16，
∴AB=AF-BF=12，
FO=
| 1 |
| 2 |
cos∠F=
| EF |
| FO |
| 4 |
| 5 |
（3）由△BEF∽△EAF，得
| BE |
| EA |
| EF |
| AF |
| 8 |
| 16 |
| 1 |
| 2 |
设BE=k，则AE=2k，
由AE2+BE2=AB2，得
（2k）2+k2=122，
解得k=
| 12 |
| 5 |
| 5 |
故BE=
| 12 |
| 5 |
| 5 |
点评：本题综合考查了相似三角形的判定与性质、勾股定理、正方形的性质以及锐角三角函数的定义等知识点．解题的关键在于根据已知条件找到相似三角形．
练习册系列答案
相关题目
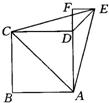16、如图所示，以正方形ABCD的对角线AC为边作等边三角形ACE，过点E作EF⊥AD，交AD的延长线于F，则∠DEF=
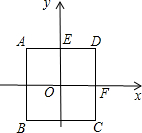如图所示，以正方形ABCD平行于边的对称轴为坐标轴建立直角坐标系，若正方形的边长为4．
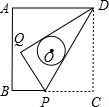已知正方形ABCD的边长为2，点P是BC上的一点，将△DCP沿DP折叠至△DPQ，若DQ，DP恰好与如图所示的以正方形ABCD的中心O为圆心的⊙O相切，则折痕DP的长为（ ）
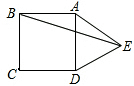如图所示，以正方形ABCD中AD边为一边向外作等边△ADE，则∠AEB=（ ）