Question

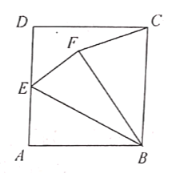
【题目】如图，正方形的边长为2，点为的中点，连接，将沿折叠，点的对应点为.连接CF，则的长为（ ）

A. B. C. D.

Answer 1

【答案】D

【解析】

连接AF交BE于点O，过点F作MN⊥AB，由勾股定理可求BE的长，由三角形面积公式可求AO的长，由折叠的性质可得AO=OH= ，AB=BF=2，由勾股定理可求BN，FN的长，由矩形的性质可求FM，MC的长，由勾股定理可求CF的长．

解：如图，连接AF交BE于点O，过点F作MN⊥AB,

∵AB∥CD，MN⊥AB,

∴MN⊥CD，

∵AB=2=AD，点E是AD中点,

∴AE=1，

∴EB=,

∵S△ABE=×AB×AE=×BE×AO,

∴2×1=AO,

∴AO=,

∵将△ABE沿BE折叠，点A的对应点为F,

∴AO=OH=，AB=BF=2，

∴AF=,

∵AF2-AN2=FN2，BF2-BN2=FN2，

∴AF2-AN2=BF2-BN2，

∴-（2-BN）2=4-BN2，

∴BN=,

∴FN=,

∵MN⊥AB，MN⊥CD，∠DCB=90°,

∴四边形MNBC是矩形,

∴BN=MC=，BC=MN=2,

∴MF=,

∴CF=.

故选：D．