题目内容
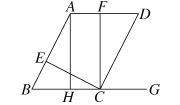
【题目】如图,已知AB∥CD,AD∥BC,∠DCE=90°,点E在线段AB上,∠FCG=90°,点F在直线AD上,∠AHG=90°.
(1)找出图中与∠D相等的角,并说明理由;
(2)若∠ECF=25°,求∠BCD的度数;
(3)在(2)的条件下,点C(点C不与B,H两点重合)从点B出发,沿射线BG的方向运动,其他条件不变,求∠BAF的度数.
【答案】(1)与∠D相等的角为∠DCG,∠ECF,∠B(2)155°(3)25°或155°
【解析】
(1)根据平行线性质和同角的余角相等可得:与∠D相等的角为∠DCG,∠ECF,∠B.
(2)由垂直定义得∠FCD=65°,所以∠BCD=65°+90°=155°.
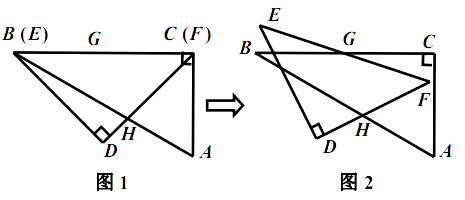
(3)分两种情况进行讨论:①如图a,当点C在线段BH上时,点F在DA的延长线上, 由AD∥BC,得∠BAF=∠B;②如图b,当点C在BH的延长线上时,点F在线段AD上.∠B=25°,AD∥BC,所以∠BAF=180°-25°=155°.
解:(1)与∠D相等的角为∠DCG,∠ECF,∠B.(1分)理由如下:
∵AD∥BC,
∴∠D=∠DCG.
∵∠FCG=90°,∠DCE=90°,
∴∠ECF=∠DCG=∠D.
∵AB∥DC,
∴∠B=∠DCG=∠D,
∴与∠D相等的角为∠DCG,∠ECF,∠B.
(2)∵∠ECF=25°,∠DCE=90°,
∴∠FCD=65°.
又∵∠BCF=90°,
∴∠BCD=65°+90°=155°.
(3)分两种情况进行讨论:
①如图a,当点C在线段BH上时,点F在DA的延长线上,此时∠ECF=∠DCG=∠B=25°.
∵AD∥BC,
∴∠BAF=∠B=25°;
②如图b,当点C在BH的延长线上时,点F在线段AD上.
∵∠B=25°,AD∥BC,
∴∠BAF=180°-25°=155°.
综上所述,∠BAF的度数为25°或155°.