题目内容
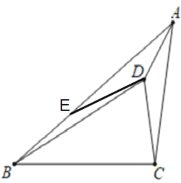
【题目】如图,在△ABC中,AB=8,AC=5,AD是∠BAC的角平分线,点D在△ABC内部,连接AD、BD、CD,∠ADB=150°,∠DBC=30°,∠ABC+∠ADC=180°,则线段CD的长度为________.

【答案】3
【解析】
在AB上截取AE=AC,证明△ADE和△ADC全等,再证BDE是等腰三角形即可得出答案.
在AB上截取AE=AC
∵AD是∠BAC的角平分线
∴∠EAD=∠CAD
又AD=AD
∴△ADE≌△ADC(SAS)
∴ED=DC,∠ADE=∠ADC
∵∠ADB=150°
∴∠EDB+∠ADE=150°
又∵∠DBC=30°,∠ABC+∠ADC=180°
∴∠ABD+∠DBC+∠ADC=180°
即∠ABD +∠ADC=150°
∴∠ABD=∠EDB
∴BE=ED
即BE=CD
又AB=8,AC=5
CD=BE=AB-AE=AB-AC=3
故答案为3

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】请你用学习“一次函数”时积累的经验和方法解决下列问题:
(1)在平面直角坐标系中,画出函数y=|x|的图象:
①列表填空:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
|
|
| … |
②描点、连线,画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|两条不同类型的性质;
(3)结合所画函数图象,求方程|x|﹣2x﹣1=0的解.