题目内容
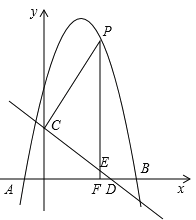
【题目】如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB 围成的图形称为该抛物线对应的准蝶形,线段AB称为碟宽,顶点M 称为碟顶.
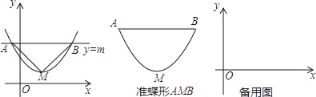
(1)由定义知,取AB中点N,连结MN,MN与AB的关系是_____.
(2)抛物线y=![]() 对应的准蝶形必经过B(m,m),则m=_____,对应的碟宽AB是_____.
对应的准蝶形必经过B(m,m),则m=_____,对应的碟宽AB是_____.
(3)抛物线y=ax2﹣4a﹣![]() (a>0)对应的碟宽在x 轴上,且AB=6.
(a>0)对应的碟宽在x 轴上,且AB=6.
①求抛物线的解析式;
②在此抛物线的对称轴上是否有这样的点P(xp,yp),使得∠APB为锐角,若有,请求出yp的取值范围.若没有,请说明理由.
【答案】(1)MN与AB的关系是:MN⊥AB,MN=![]() AB,(2)2,4;(3)①y=
AB,(2)2,4;(3)①y=![]() x2﹣3;②在此抛物线的对称轴上有这样的点P,使得∠APB 为锐角,yp的取值范围是yp<﹣3或yp>3.
x2﹣3;②在此抛物线的对称轴上有这样的点P,使得∠APB 为锐角,yp的取值范围是yp<﹣3或yp>3.
【解析】
(1)直接利用等腰直角三角形的性质分析得出答案;
(2)利用已知点为B(m,m),代入抛物线解析式进而得出m的值,即可得出AB的值;
(3)①根据题意得出抛物线必过(3,0),进而代入求出答案;
②根据y=![]() x2﹣3的对称轴上P(0,3),P(0,﹣3)时,∠APB 为直角,进而得出答案.
x2﹣3的对称轴上P(0,3),P(0,﹣3)时,∠APB 为直角,进而得出答案.
(1)MN与AB的关系是:MN⊥AB,MN=![]() AB,
AB,
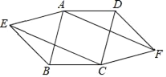
如图1,∵△AMB是等腰直角三角形,且N为AB的中点,
∴MN⊥AB,MN=![]() AB,
AB,
故答案为:MN⊥AB,MN=![]() AB;
AB;

(2)∵抛物线y=![]() 对应的准蝶形必经过B(m,m),
对应的准蝶形必经过B(m,m),
∴m=![]() m2,
m2,
解得:m=2或m=0(不合题意舍去),
当m=2则,2=![]() x2,
x2,
解得:x=±2,
则AB=2+2=4;
故答案为:2,4;
(3)①由已知,抛物线对称轴为:y轴,
∵抛物线y=ax2﹣4a﹣![]() (a>0)对应的碟宽在x 轴上,且AB=6.
(a>0)对应的碟宽在x 轴上,且AB=6.
∴抛物线必过(3,0),代入y=ax2﹣4a﹣![]() (a>0),
(a>0),
得,9a﹣4a﹣![]() =0,
=0,
解得:a=![]() ,
,
∴抛物线的解析式是:y=![]() x2﹣3;
x2﹣3;
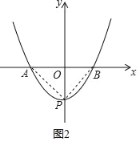
②由①知,如图2,y=![]() x2﹣3的对称轴上P(0,3),P(0,﹣3)时,∠APB 为直角,
x2﹣3的对称轴上P(0,3),P(0,﹣3)时,∠APB 为直角,
∴在此抛物线的对称轴上有这样的点P,使得∠APB 为锐角,yp的取值范围是yp<﹣3或yp>3.

 阅读快车系列答案
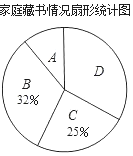
阅读快车系列答案【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.