题目内容
等腰梯形的上底长为2cm,下底长为10cm,高为3cm,则它的腰长为分析:首先作等腰梯形的两条高,易得四边形AEFD是矩形,Rt△ABE≌Rt△DCF;根据题意,可得BE=CF=4cm,由勾股定理,即可求得等腰梯形的腰长.
解答: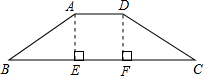 解:
解:
过点A作AE⊥BC于E,过点D作DF⊥BC于F,
∴AE∥DF,∠AEB=∠DFC=90°,
∵AD∥BC,
∴四边形AEFD是矩形,
∴AD=EF,AE=DF,
∵AB=CD,
∴Rt△ABE≌Rt△DCF(HL),
∴BE=CF,
∴BE=CF=
(BC-AD)=
×(10-2)=4(cm),
∵AE=3cm,
∴AB=5cm.
 解:
解:过点A作AE⊥BC于E,过点D作DF⊥BC于F,
∴AE∥DF,∠AEB=∠DFC=90°,
∵AD∥BC,
∴四边形AEFD是矩形,
∴AD=EF,AE=DF,
∵AB=CD,
∴Rt△ABE≌Rt△DCF(HL),
∴BE=CF,
∴BE=CF=
| 1 |
| 2 |
| 1 |
| 2 |
∵AE=3cm,
∴AB=5cm.
点评:此题考查了等腰梯形的性质、矩形的判定与性质、全等三角形的判定与性质等知识.解此题的关键是注意过梯形的两个顶点作梯形的两条高是解答梯形题目中的常见辅助线.

练习册系列答案
相关题目
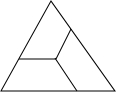 如图,用三个全等的等腰梯形拼接成一个边长为a的等边三角形,则每个等腰梯形的上底长为
如图,用三个全等的等腰梯形拼接成一个边长为a的等边三角形,则每个等腰梯形的上底长为